Основные формулы преобразования степеней и корней

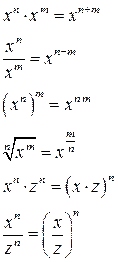
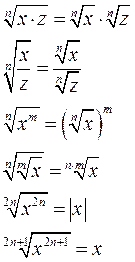
Напомним, что записанные равенства справедливы только на общей части ОДЗ для буквенных величин, входящих в выражения, стоящие в левой и в правой частях каждого равенства.

Показательная функция

Показательной функциейаргумента х называется функция вида

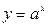, где a > 0, a ¹ 1

Графики показательных функций различаются по условиям a > 1 или
0 < a < 1, (рис. 65).

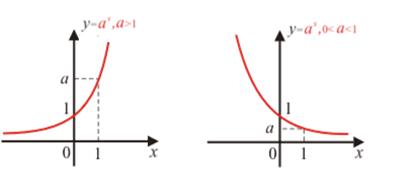Рис. 65

ООФ: 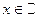ОЗФ:

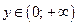
Логарифмическая функция

Логарифмическая функцияимеет вид 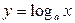, где a > 0, a ¹ 1.
Напомним, что логарифмом числа х по основанию аназывается такой показатель степени у, что 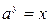, то есть .

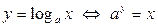Из определения логарифма следует, что логарифмическая и функции являются взаимно обратными. Графики логарифмических функций различаются, как и графики показательных функций по условиям a > 1 или 0 < a < 1, (рис. 66)

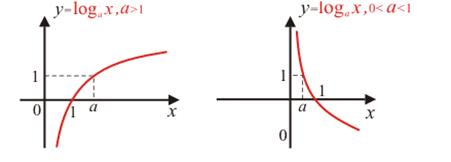Рис. 66

ОО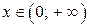Ф: ОЗФ: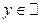

Основные формулы преобразования логарифмов

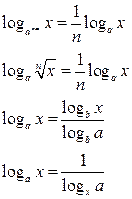
При использовании этих формул необходимо помнить о требовании совпадения ОДЗ для выражений, стоящих в левой и в правой частях каждого равенства.