Несчетность множества действительных чисел
Легко показать, что множество 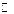 всех действительных чисел имеет такую же мощность, как и множество чисел промежутка
всех действительных чисел имеет такую же мощность, как и множество чисел промежутка 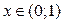 . Действительно, биективное отображение этих множеств легко устанавливается с помощью непрерывной монотонной функции, определенной на одном из этих множеств и принимающей все значения другого множества, (рис. 39).
. Действительно, биективное отображение этих множеств легко устанавливается с помощью непрерывной монотонной функции, определенной на одном из этих множеств и принимающей все значения другого множества, (рис. 39).

Рис.39
Теперь будем доказывать несчетность множества чисел 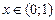 . Заметим, что доказать несчетность какого-то множества нелегко. Ведь доказательство счетности множества сводится просто к придумыванию правила, по которому нумеруются все его элементы. А доказать несчетность какого-то множества — это значит доказать, что такого правила нет и быть не может. Иными словами, какое бы правило мы ни придумали, всегда найдется незанумерованный элемент этого множества.
. Заметим, что доказать несчетность какого-то множества нелегко. Ведь доказательство счетности множества сводится просто к придумыванию правила, по которому нумеруются все его элементы. А доказать несчетность какого-то множества — это значит доказать, что такого правила нет и быть не может. Иными словами, какое бы правило мы ни придумали, всегда найдется незанумерованный элемент этого множества.
Для доказательства несчетности множества 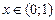 будем использовать так называемый «диагональный метод», оригинально предложенный Кантором в 1891г.
будем использовать так называемый «диагональный метод», оригинально предложенный Кантором в 1891г.
Предположим противное, то есть предположим счетность множества 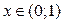 ; это означает, что все числа промежутка
; это означает, что все числа промежутка 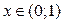 можно занумеровать в некоторую счетную последовательность
можно занумеровать в некоторую счетную последовательность 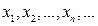 . Известно, что каждое действительное число
. Известно, что каждое действительное число 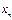 можно записать в виде бесконечной десятичной дроби; будем использовать эту запись для чисел
можно записать в виде бесконечной десятичной дроби; будем использовать эту запись для чисел 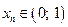 :
:
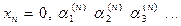 ,
,
где 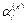 — это любые из цифр 0, 1, ... , 9, взятые в любом порядке.
— это любые из цифр 0, 1, ... , 9, взятые в любом порядке.
Теперь будем строить новое число 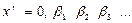 следующим образом:
следующим образом:
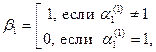
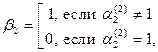
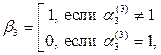 …
…
 , …
, …

Например, если то 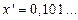
Очевидно, что число 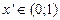 и отличается от всех чисел
и отличается от всех чисел 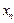 , потому что:
, потому что:
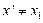 , так как отличается от
, так как отличается от 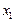 первой цифрой после запятой,
первой цифрой после запятой,
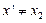 , так как отличается от
, так как отличается от 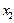 второй цифрой после запятой,
второй цифрой после запятой,
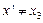 , так как отличается от
, так как отличается от 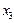 третьей цифрой после запятой, и т.д.
третьей цифрой после запятой, и т.д.
Таким образом, число 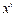 не попало в счетную последовательность
не попало в счетную последовательность 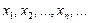 по какому правилу бы мы ее ни составляли.
по какому правилу бы мы ее ни составляли.
Очевидно, что аналогичных «незанумерованных» чисел построить можно сколько угодно, например, заменяя цифры 1 и 0 на другие цифры. Следовательно, предположение о возможности занумеровать все числа 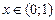 является неверным. Из этого следует, что множество
является неверным. Из этого следует, что множество 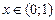 не является счетным, но имеет бо́льшую мощность, чем мощность счетного множества.
не является счетным, но имеет бо́льшую мощность, чем мощность счетного множества.
Мощность множества 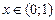 , а также эквивалентного ему множества
, а также эквивалентного ему множества 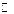 называется мощностью континуум. Легко доказывается, что такую же мощность имеют любые непрерывные подмножества множества
называется мощностью континуум. Легко доказывается, что такую же мощность имеют любые непрерывные подмножества множества 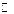 . Для этого достаточно построить биективное отображение заданного непрерывного множества
. Для этого достаточно построить биективное отображение заданного непрерывного множества 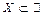 на промежуток
на промежуток 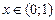 или на все множество
или на все множество 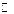 .
.
Дата добавления: 2021-07-22; просмотров: 504;











