Упражнения для самостоятельной работы
1. Найдите образ 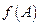 множества
множества 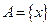 при отображении функцией
при отображении функцией 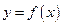 :
:
1) 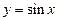 ,
, 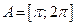 ; 2)
; 2) 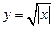 ,
, 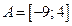 ; 3)
; 3) 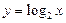 ,
, 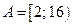 ;
;
4) 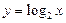 ,
, 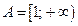 ; 5)
; 5) 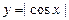 ,
, 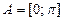 ; 6)
; 6) 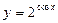 ,
, 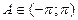 .
.
2. Найдите прообраз множества 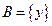 при отображении функцией
при отображении функцией 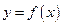 :
:
1) 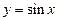 ,
, 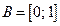 ; 2)
; 2) 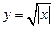 ,
, 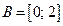 ; 3)
; 3) 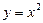 ,
, 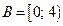 ;
;
4) 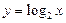 ,
, 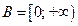 ; 5)
; 5) 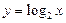 ,
, 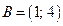 ; 6)
; 6) 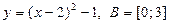 .
.
3. Составьте суперпозиции отображений 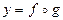 и
и 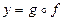 для заданных функций
для заданных функций 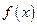 и
и 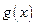 и укажите множество задания и множество значений каждого из составленных отображений:
и укажите множество задания и множество значений каждого из составленных отображений:
1) 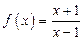 ,
, 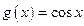 ; 2)
; 2) 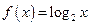 ,
, 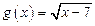 .
.
4.Запишите суперпозиции функций 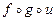 ,
, 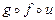 ,
, 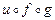 , если
, если 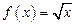 ,
, 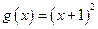 ,
, 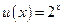 ; укажите отображения множеств, которые задают составленные сложные функции.
; укажите отображения множеств, которые задают составленные сложные функции.
Ответы к упражнениям для самостоятельной работы
1. 1) 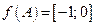 ; 2)
; 2) 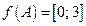 ; 3)
; 3) 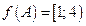 ; 4)
; 4) 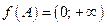 ; 5)
; 5) 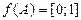 ; 6)
; 6) 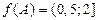 .
.
2. 1) 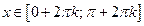 ,
, 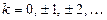 ; 2)
; 2) 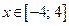 ;
;
3) 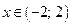 ; 4)
; 4) 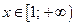 ;
;
5) 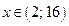 ; 6)
; 6) 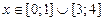 .
.
3. 1) 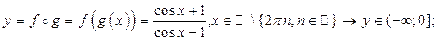
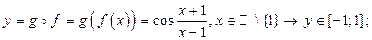
2) 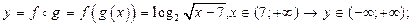
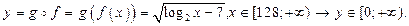

4. , 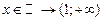 ;
;

, 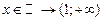 ;
;

, 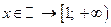 .
.
Вопросы для самопроверки
Что такое понятие соответствия?
Что такое отображения множеств или функции?
Что называется отображением множества X в множество Y или функцией, определенной на множестве X и принимающей значения в множестве Y?
Что называется независимой переменной, или аргументом функции?
Что называется зависимой переменной?
Что такое функциональная зависимость?
Что называется множеством задания функции?
Что называется множеством значений функции?
Что такое функция Дирихле?
Что называется отображением множества X на множество Y, или сюръекцией?
Что называется инъекцией?
Что называется биекцией?
Что называется взаимно однозначным отображением?
Что называется образом множества А при отображении f?
Что называется прообразом множества В при отображении f?
Что называется многозначным отображением?
Что называется обратным отображением?
Что называется обратной функцией?
Что называется взаимно обратными функциями?
Что называется суперпозицией отображений f и g?
Что такое композиция отображений, сложное отображение?
Глоссарий
понятие соответствия это…(стр. 49)
отображением множества X в множество Y или функцией, определенной на множестве X и принимающей значения в множестве Y называется…(стр. 49)
независимой переменной, или аргументом функции называется…(стр. 50)
зависимой переменной называется…(стр. 50)
функциональная зависимость называется…(стр. 50)
множеством задания функции называется…(стр. 51)
множеством значений функции называется…(стр. 51)
функция Дирихле это…(стр. 52)
отображением множества X на множество Y, или сюръекцией называется…(стр. 52)
инъекцией называется…(стр. 52)
биекцией называется…(стр. 52)
взаимно однозначным отображением называется…(стр. 53)
образом множества А при отображении f называется…(стр. 53)
прообразом множества В при отображении f называется…(стр. 54)
многозначным отображением называется…(стр. 55)
обратным отображением называется…(стр. 55)
обратной функцией называется…(стр. 56)
взаимно обратными функциями называется…(стр. 56)
суперпозицией отображений f и g называется…(стр. 57)
композиция отображений, сложное отображение это…(стр. 57)
Дата добавления: 2021-07-22; просмотров: 430;











