Понятие мощности множества

Основателем учения о множествах является немецкий математик Георг Кантор (G. Kantor, 1845-1918), профессор из Галле. Одной из великих заслуг Кантора является то, что он установил точные понятия, возникающие в задаче сравнения бесконечных множеств по величине или по объему. Эта задача является тривиальной для конечных множеств и решается сравнением количеств элементов в них. Но для бесконечных множеств задача их сравнения приводит к непростой проблеме: можно ли бесконечное количество элементов одного множества считать большим, равным или меньшим бесконечному количеству элементов другого множества? По предложению Кантора, сравнение двух множеств осуществляется описанием взаимно однозначного соответствия между их элементами.

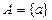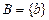Говорят, что можно установить взаимно однозначное соответствие между элементами двух множеств и (биекцию), если:

1) каждому элементу 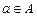соответствует единственный элемент ;

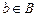2) каждый элемент 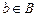является соответствующим единственному элементу .

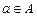Определение эквивалентных множеств

Два множества, между элементами которых можно установить взаимно однозначное соответствие (биекцию), называются равномощными множествами, или множествами, имеющими одинаковую мощность, или эквивалентными множествами по мощности. Обозначение эквивалентных (равномощных) множеств:

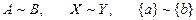
Таким образом, между элементами равномощных (эквивалентных) множеств всегда существует биективное отображение. Если же такое отображение установить невозможно, то множества имеют различную мощность; при этом оказывается, что каким бы образом мы ни пытались бы привести в соответствие друг другу элементы двух множеств, всегда останутся лишние элементы и притом всегда от одного и того же множества, которое имеет поэтому бо́льшую мощность. Если эти определения применить к конечным множествам, то получим следующее:

два конечных множества равномощны тогда и только тогда, когда они содержат одинаковое количество элементов;

из двух конечных множеств 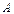и 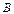, у которых 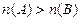, большую мощность имеет множество 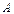, содержащее большее количество элементов;

всякое конечное множество 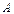всегда имеет большую мощность, чем любое его собственное подмножество .

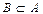Примеры (сравнение конечных множеств)

1)

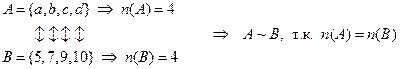
т.е. множества A и B имеют одинаковую мощность или являются эквивалентными по мощности;

знаком ↔ обозначено взоимно однозначное соответствие между элементами двух множеств;

2)

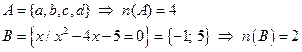
множество А имеет бо́льшую мощность, чем множество B, так как ;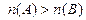

множество В имеет меньшую мощность, чем множество А, так как ;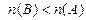

3)

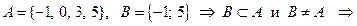
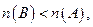
то есть собственное подмножество В конечного множества А имеет меньшую мощность, чем само множество А.

Множество, которое не является конечным, называется бесконечным и количество элементов в нем не может быть выражено никаким числом. Поэтому сравнить бесконечные множества можно только по их мощности, то есть с помощью процедуры, устанавливающей взаимно однозначное соответствие между элементами этих множеств.

Примеры (эквивалентные бесконечные множества)

1) ,

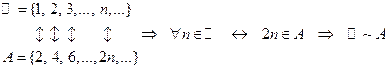то есть множество 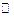всех натуральных чисел имеет такую же мощность, как и его собственная часть, состоящая только из четных чисел;

2) ,

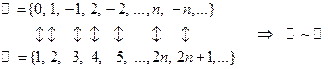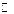то есть множество всех целых чисел и множество 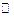всех натуралных чисел имеют одинаковую мощность;

3)

Рис. 36

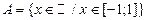
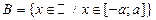
бесконечные множества 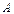и 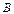эквивалентны (имеют одинаковую мощность), так как между их элементами легко устанавливается взаимно однозначное соответствие так, как показано на рисунке 36; таким образом, множества точек на отрезках разной длины имеют одинаковую мощность;

4) ,

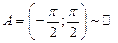так как между элементами этих бесконечных множеств устанавливается взаимно однозначное соответствие, например, с помощью графика функции 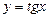, , 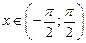(рис. 37);

таким образом, множество 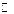всех действительных чисел имеет одинаковую мощность с множеством точек интервала .

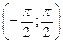Рассмотренные примеры убедительно показывают, что собственная часть (собственное подмножество) бесконечного множества может иметь равную с ним мощность, то есть для бесконечных множеств не является верным утверждение «часть меньше целого».

Счётные множества

Определение счетного множества

Множество 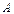называется счетным множеством, если оно эквивалентно (равномощно) множеству натуральных чисел: 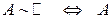– счетное множество

Например, счетными множествами являются следующие множества:

1) 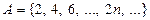— множество натуральных четных чисел;

2) 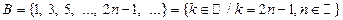— множество натуральных нечетных чисел;

3) 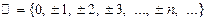— множество целых чисел;

4) 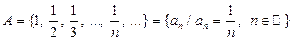— множество членов последовательности с общим членом ;

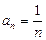5) 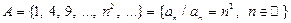— множество членов последовательности с общим членом .

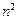Из определения счетного множества и рассмотренных примеров следует, что отличительная особенность счетного множества состоит в том, что все его элементы можно занумеровать.

Доказательство счетности множества рациональных чисел

Для доказательства счетности множества рациональных чисел

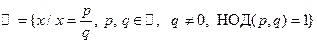
необходимо предложить способ нумерации его элементов, то есть процедуру, в которой каждому рациональному числу будет присвоен единственный натуральный номер. Такую процедуру удается построить для положительных рациональных чисел следующим образом: выпишем сначала все положительные дроби со знаменателем 1, потом следующей строкой запишем все положительные дроби со знаменателем 2, потом со знаменателем 3 и т.д. Получится таблица, изображенная на рисунке 38 а).

а)

б)

Ясно, что в этой таблице находится любое положительное рациональное число, и притом не один раз. Например, число 3 встретится в виде дробей 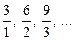, число 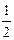также встретится в виде нескольких дробей: .

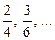Будем нумеровать представленные в таблице числа «по квадратам», начиная с левого верхнего угла и присваивая номер каждому следующему числу, отличному от всех предыдущих (каждой несократимой дроби). Эта нумерация представлена на рис. 38 б).

В результате получаем следующую занумерованную последовательность всех положительных рациональных чисел:

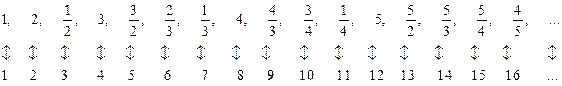
Теперь уже легко понять, как нумеруются все рациональные числа — ноль, положительные и отрицательные. Их нужно расположить на основании предыдущей последовательности следующим образом:

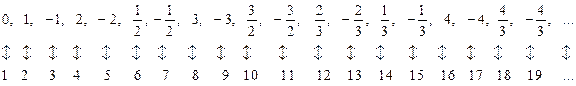
Это расположение устанавливает взаимно однозначное соответствие между элементами множества рациональных чисел 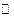и элементами множества натуральных чисел 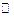. Следовательно, эти множества имеют одинаковую мощность: 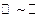, поэтому множество 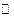является счетным, что и требовалось доказать.