Е). Система полярных координат

Систему полярных координат применяют при определении планового положения точек на небольших участках местности в процессе съёмки и при геодезических разбивочных работах.

В этой системе координат положение точки определяется относительно полюса О и направления полярной оси ОА ( рисунок 6).

А

О

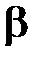
D

В

Рисунок 9 Система полярных координат

Полярными координатами точки В будут угол 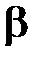и полярное расстояние D.

Системы высот

Счет высот в геодезии ведут от одной из уровенных поверхностей.

Высотой точки называют расстояние по отвесной линии от точки до уровенной поверхности, принятой за начало счета высот.

Если высоты отсчитывают от основной уровенной поверхности, то есть от поверхности геоида, их называют абсолютными высотами. На рис. 7 отрезки отвесных линий Аа и Вв - абсолютные высоты точек А и В.

Если за начало счета высот выбрана какая-либо другая уровенная поверхность, то высоты называют условными. На рис. 7 отрезки отвесных линий Аа¢ и Вв¢ - условные высоты точек А и В.

В России принята Балтийская система высот. Счет абсолютных высот ведут от уровенной поверхности, проходящей через нуль Кронштадтского футштока.

Численное значение высоты принято называть отметкой. Например, если высота точки А равна H_А = 15,378 м, то говорят, что отметка точки равна 15,378 м.

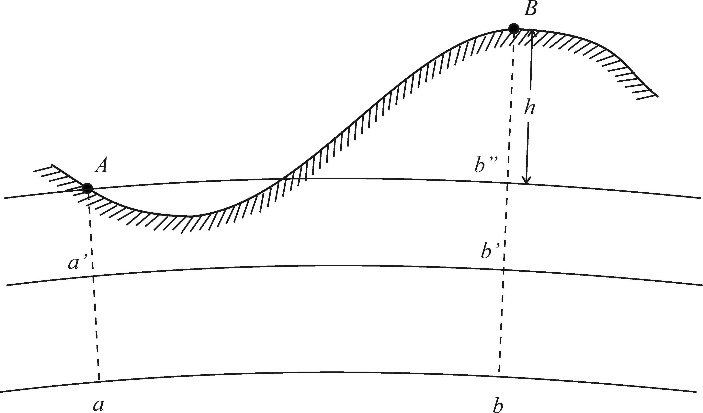
Рис. 10 Абсолютные и условные высоты: a¢b¢ – уровенная поверхность; ab –поверхность геоида; Ab² – уровенная поверхность точки A;

Разность высот двух точек называется превышением. Так, превышение точки В над точкой А равно

h_AB = H_В - H_A.

Зная высоту точки А, для определения высоты точки В на местности измеряют превышение h_AB. Высоту точки В вычисляют по формуле

H_В = H_A + h_AB.

Измерение превышений и последующее вычисление высот точек называется нивелированием.

Абсолютную высоту точки следует отличать от ее геодезической высоты, то есть высоты, отсчитываемой от поверхности земного эллипсоида (см. раздел 2.2). Геодезическая высота отличается от абсолютной высоты на величину отклонения поверхности геоида от поверхности эллипсоида.

В заключение отметим, что точное определение положения поверхности геоида в области материков невозможно. Поэтому в России принято отсчитывать высоты от близкой к геоиду, но доступной точному определению вспомогательной поверхности, названной квазигеоидом. Высоты, отсчитываемые от поверхности геоида, называются ортометрическими высотами, а отсчитываемые от поверхности квазигеоида – нормальными высотами. На результаты измерений, выполняемых в инженерной геодезии, различия в двух названных системах высот влияния не оказывают, и в дальнейшем мы их различать не будем, а будем пользоваться введенным выше обобщенным понятием – абсолютные высоты.