Предмет и задачи геодезии.

Задачи инженерной (прикладной) геодезии.

Этапы развития геодезии.

ФОРМА И РАЗМЕРЫ ЗЕМЛИ. СИСТЕМЫ КООРДИНАТ.

ВЫСОТЫ.

Фигура Земли сформировалась под воздействием многих процессов, связанных с её образованием и существованием. Решающее значение при этом имеют силы внутреннего тяготения и центробежные.

Если бы земля была однородна и неподвижна, то под действием сил только внутреннего тяготения, как фигура равновесия, она бы имела форму шара. Так, для приближенных вычислений Землю принимают за шар с радиусом 6371 км.

В результате действия центробежной силы, вызванной вращением Земли вокруг своей оси, Земля приобрела форму земного сфероида, сплюснутого у полюсов.

Представить фигуру Земли в качестве сфероида можно с большим обобщением. Реальная поверхность Земли - это поверхность материков, дна морей и океанов. Она сложна и напоминает сфероид лишь в целом.

Поэтому изучение формы и размеров Земли включает решение двух задач. Это - установление некоторой сглаженной, обобщенной, теоретической фигуры Земли и определение отклонений от нее фактической физической поверхности.

Учитывая, что поверхность океанов и морей составляет 71% поверхности Земли, а поверхность суши - только 29%, за теоретическую фигуру Земли принято тело, ограниченное поверхностью океанов в их спокойном состоянии, продолженной и под материками.

Для изучения фигуры Земли введено понятие уровенной поверхности.

Уровенная поверхность – поверхность, на которой потенциал силы тяжести Земли всюду имеет одно и то же значение.

С геометрической точки зрения У.П. – поверхность, пересекающая отвесные линии во всех точках под прямым углом; с физической точки зрения – поверхность, во всех точках которой значение потенциала силы тяжести W одно и то же, т.е. W=C.

Физическая поверхность Земли

М

900

900

Эллипсоид

Основная уровенная поверхность (((геоид)

Отвесная линия

Нормаль

u

Рис. 1

N

Фигура Земли, образованная основной уровенной поверхностью, мысленно продолженной под всеми материками и континентами, называется г е о и д о м.

 

 

 

Из-за неравномерности распределения масс в земной коре геоид имеет неправильную геометрическую форму, и его поверхность нельзя выразить математически (Рис. 2), что необходимо для решения геодезических задач. При решении геодезических задач геоид заменяют близкими к нему геометрически правильными поверхностями.

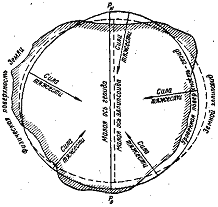
Рис. 2

Ближе к форме геоида подходит эллипсоид – фигура, получаемая вращением эллипса (рис. 2) вокруг его малой оси.

Размеры земного эллипсоида характеризуют следующими основными параметрами: a - большая полуось, b - малая полуось, a - полярное сжатие и e – первый эксцентриситет меридианного эллипса, где 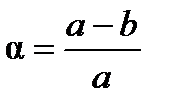и .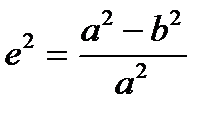

 

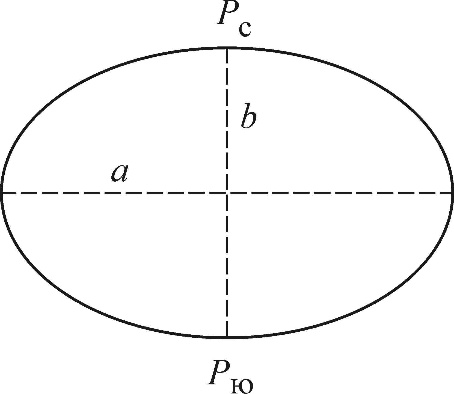
Рис. 3 Меридианный эллипс: Рс – северный полюс; Рю – южный полюс

 

Различают общеземной эллипсоид и референц-эллипсоид.

Центр общеземного эллипсоида помещают в центре масс Земли, ось вращения совмещают со средней осью вращения Земли, а размеры принимают такие, чтобы обеспечить наибольшую близость поверхности эллипсоида к поверхности геоида.

Общеземной эллипсоид используют при решении глобальных геодезических задач, и в частности, при обработке спутниковых измерений. В настоящее время широко пользуются двумя общеземными эллипсоидами: ПЗ-90 (Параметры Земли 1990 г, Россия) и WGS-84 (Мировая геодезическая система 1984 г, США).

Референц-эллипсоид – эллипсоид, принятый для геодезических работ в конкретной стране. С референц-эллипсоидом связана принятая в стране система координат. Параметры референц-эллипсоида подбираются под условием наилучшей аппроксимации данной части поверхности Земли. При этом совмещения центров эллипсоида и Земли не добиваются.

В России с 1946 г. в качестве референц-эллипсоида используется эллипсоид Красовскогос параметрами: а = 6 378 245 м, a = 1/ 298,3.

Параметры эллипсоида Красовского получены по результатам обработки геодезических измерений, выполненных на территории СССР в период с 1925 по 1940 год и введены в действие постановлением Совета Министров СССР №746 от 20 апреля 1946 года.