Уравнение гидростатики

Умножим каждый из членов, входящих в систему (13) дифференциальных уравнений, соответственно на 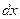; ; 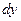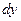и просуммируем их. В результате этих действий получим:

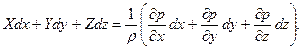(14)

Уравнение (14) является аналитическим выражением распределения гидростатического давления жидкости.

Для случая покоящейся жидкости гидростатическое давление 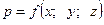. Следовательно, правая часть уравнения (14) представляет полный дифференциал давления .

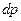Таким образом, приведенное выше уравнение (14) приобретает следующий вид:

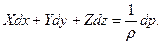(15)

Применим уравнение (15) к случаю абсолютного покоя жидкости, когда массовой силой является только сила тяжести. При принятом направлении координатных осей проекции этой силы будут:

; ; ,

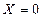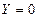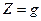а уравнение (15) применительно к точке получает вид:

.

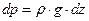После интегрирования получим:

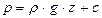
При 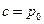– давление на свободной поверхности, а 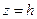– глубина погружения в жидкости точки, для которой определяется давление:

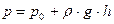(16)

где		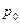– давление на свободной поверхности;
		– плотность жидкости.

Уравнение (16) называется основным уравнением гидростатики.

Закон Паскаля

«Если жидкость находится в состоянии покоя, то изменение давления на любой внешней поверхности, возникающее от действия внешних сил, передается без изменения во все точки объема, занимаемого данной жидкостью».

Доказательство из уравнения (16).

Абсолютное давление в т. А при размещении поршня в положении – 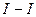(рис.3):

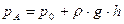(17)

После перемещения поршня в положение 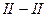(рис. 3а) давление на свободной поверхности увеличится на величину 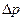и будет равно 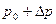, а абсолютное давление в т. А будет равно

,

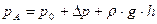т.е. при изменении давления на свободной поверхности на 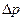, на эту же величину увеличится давление в точке А.

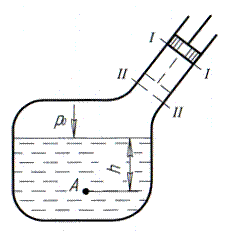
Рис. 3а. Схема действия давления по закону Паскаля.

Эта идея использована Паскалем в принципиальной концепции гидропроцесса.