Частотный критерий устойчивости Михайлова.

Критерий Михайлова предполагает построение годографа на комплексной плоскости. Для построения годографа из уравнения (4.1) путем подстановки S=jw получают аналитическое выражение вектора D(jw):

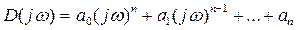(4.2)

Уравнение (4.2) является комплексным и может быть представлено в виде:

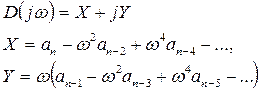где

Построение годографа производится по уравнению вектора D(jw) при изменении частою от 0 до ¥.

Для случая устойчивости системы n-го порядка необходимо и достаточно, чтобы при w = 0 годограф начинался на вещественной положительной оси и обходил против часовой стрелки n квадран­тов, нигде не обращаясь в нуль.

Если годограф начинается в нулевой точке комплексной плоскости или проходит через эту точку при определенной частоте, то система считается нейтральной.

Частотный критерий устойчивости Найквиста.

Данный критерий позволяет по амплитудно-фазовой частотной характеристике разомкнутой системы оценить устойчивость системы. АФЧХ может быть получена экспериментально или аналитически. Аналитическое построение АФЧХ производится обычными методами.

Для устойчивости замкнутой системы необходимо и достаточно, чтобы АФЧХ разомкнутой системы при изменении частоты от 0 до ¥ не охватывала точку с координатами –I, j0. Если АФЧХ разомкнутой системы проходитчерез точку с координатами –I, j0, то система будет нейтральной.

Критерий Найквиста позволяет наглядно проследить влияние изменения параметров передаточной функции на устойчивость системы.