Структурные схемы и структурные преобразования.

Обычно структурная схема САР состоит из отдельных элементов, соединенных последовательно, параллельно или с помощью обратных связей. Каждый элемент имеет один вход и один выход и заданную передаточную функцию.

Существуют следующие правила структурных преобразований, позволяющие по передаточным функциям отдельных элементов опреде­лить требуемую передаточную функцию.

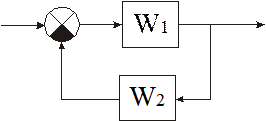
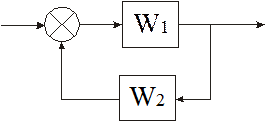
При последовательном соединении элементов передаточные функции перемножаются. При параллельном соединении передаточные функции суммируются. Правила структурных преобразований при наличии обратных связей представлены на рис 2.2.

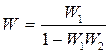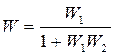Рис2.2. Правила структурных преобразований при наличии обратных связей: а - положительная, б - отрицательная.

Рассмотренные правила позволяют для одноконтурных структур САР получить эквивалентные передаточные функции по управлению, по возмущению, по ошибке и разомкнутой САР.

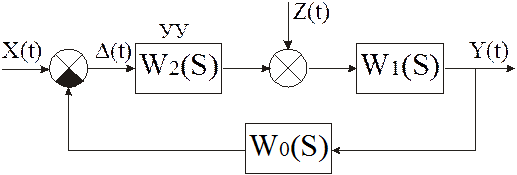Пусть задана структура одноконтурной САР в виде, представленном на рис 2.3

Рис 2.3. Структурная схема одноконтурной САР.

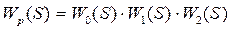Передаточная функция разомкнутой системы W_p ( S ) определя­ется выражением:

Передаточная функция замкнутой САР по управлению W_y(S) имеет следующий вид:

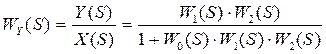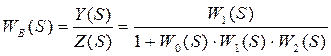Передаточная функция замкнутой САР по возмущению определяется выражением:

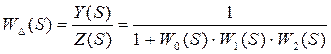Передаточная функция замкнутой САР по ошибке имеет следующий вид.

Приведенные здесь передаточные функции получены на основе применения правила последовательного соединения элементов и соединения в виде обратных связей.

Если задана многоконтурная структура САР, то с помощью структурных преобразований она может быть приведена к одноконтурной. При этом используется ряд дополнительных правил, связанных с переносом элементов структурной схемы. Эти правила сведены в таблицу 2.1.

Таблица 2.1