Глава 2. Методы многомерной безусловной оптимизации
Основные понятия
К задачам многомерной безусловной оптимизации относятся задачи нахождения экстремума функции нескольких переменных без ограничения на возможные значения этих переменных. В общем случае задача состоит в том, чтобы отыскать x* Î En, для которого выполнено условие
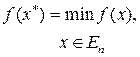 (2.1.1)
(2.1.1)
где x = (x1, x2, …, xn)т – вектор варьируемых параметров x1, x2, …, xn;
n – размерность вектора х; f(x) – вещественная скалярная функция векторного аргумента или функция n-переменных; En – n-мерное евклидово пространство.
Как и для задач одномерной оптимизации, часто используется следующая терминология:
– f(x) – функция цели или целевая функция;
– "x Î En – решение задачи (2.1.1);
– x* – оптимальное решение задачи (2.1.1).
Задачу (2.1.1) называют задачей безусловной многомерной оптимизации, так как на значения компонент векторного аргумента x
не накладывается никаких условий.
Решить задачу (2.1.1) – значит найти ее оптимальное решение. Отметим, что, как и в случае задачи одномерной оптимизации,
для нахождения максимума функции j(x) достаточно взять функцию
f(x) = –j(x) и решить задачу по нахождению минимума функции f(x) на En. Поэтому рассмотрение задачи минимизации (2.1.1) не умаляет общности.
Методы многомерной безусловной оптимизации, как и методы одномерной безусловной оптимизации, являются итерационными. С их помощью строят 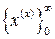 – в общем случае бесконечную последовательность точек x(k) Î En, k = 0, 1, 2, …, сходящуюся при выполнении условий сходимости к x* Î En – точке, отвечающей оптимальному решению задачи (2.1.1). В дальнейшем последовательность
– в общем случае бесконечную последовательность точек x(k) Î En, k = 0, 1, 2, …, сходящуюся при выполнении условий сходимости к x* Î En – точке, отвечающей оптимальному решению задачи (2.1.1). В дальнейшем последовательность 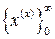 , в которой каждый элемент х(k) Î En, k = 0, 1, 2, … является вектором, будем также называть векторной.
, в которой каждый элемент х(k) Î En, k = 0, 1, 2, … является вектором, будем также называть векторной.
Определение 2.1.1.
Итерационный метод сходится, если генерируемая в процессе его работы векторная последовательность 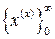 сходится к х* – искомому решению, т. е. выполнено условие
lim х(k) = х*. (2.1.2)
k ® ¥
В противном случае, метод расходится. сходится к х* – искомому решению, т. е. выполнено условие
lim х(k) = х*. (2.1.2)
k ® ¥
В противном случае, метод расходится.
|
Можно дать различные определения сходимости векторной последовательности 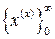 к x* Î En.
к x* Î En.
Определение 2.1.2
Последовательность 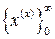 сходится к х* – искомому решению, если выполнено условие сходится к х* – искомому решению, если выполнено условие
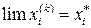 , i = 1, 2, …, n. (2.1.3)
k ® ¥ , i = 1, 2, …, n. (2.1.3)
k ® ¥
|
Согласно этому определению сходимость векторной последовательности естественным образом находится через сходимость числовых последовательностей, которые образуются каждой отдельной компонентой векторов, составляющих векторную последовательность.
Чаще используется эквивалентное предыдущему определение сходимости векторной последовательности в терминах норм векторов:
Определение 2.1.2*
Последовательность 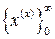 сходится к х* – искомому решению, если выполнено условие сходится к х* – искомому решению, если выполнено условие
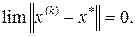 (2.1.4)
k ® ¥ (2.1.4)
k ® ¥
|
Напомним, что в евклидовом пространстве вводится так называемая евклидова норма вектора
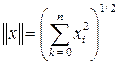 . (2.1.5)
. (2.1.5)
Как отмечалось выше (см. гл. 1), понятие скорости сходимости итерационного метода является не менее важным, чем понятие сходимости. Для многомерного случая переформулируем определение скорости сходимости в терминах норм векторов.
Определение 2.1.3
Пусть х* – искомое решение и сходящийся итерационный метод генерирует в процессе работы векторную последовательность 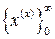 . Тогда будут справедливы следующие утверждения:
1. Метод сходится к х* с линейной скоростью (или со cкоростью геометрической последовательности), если для всех k, начиная с некоторого k* ³ 0 и 0 £ q < 1, выполнено условие
ççх(k +1) – х*êç £ q ççх(k) – х*êç. (2.1.6)
2. Метод сходится к х* со сверхлинейной скоростью, если для всех k, начиная с некоторого k* ³ 0, выполнено условие
ççх(k +1) – х*êç £ qkççх(k) – х*êç, (2.1.7)
где числовая последовательность . Тогда будут справедливы следующие утверждения:
1. Метод сходится к х* с линейной скоростью (или со cкоростью геометрической последовательности), если для всех k, начиная с некоторого k* ³ 0 и 0 £ q < 1, выполнено условие
ççх(k +1) – х*êç £ q ççх(k) – х*êç. (2.1.6)
2. Метод сходится к х* со сверхлинейной скоростью, если для всех k, начиная с некоторого k* ³ 0, выполнено условие
ççх(k +1) – х*êç £ qkççх(k) – х*êç, (2.1.7)
где числовая последовательность 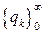 сходится к нулю.
3. Метод сходится к х* с квадратической скоростью, если для всех k, начиная с некоторого k* ³ 0 и q ³ 0, выполнено условие
ççх(k + 1) – х*çê £ qççх(k) – х*êç2. (2.1.8) сходится к нулю.
3. Метод сходится к х* с квадратической скоростью, если для всех k, начиная с некоторого k* ³ 0 и q ³ 0, выполнено условие
ççх(k + 1) – х*çê £ qççх(k) – х*êç2. (2.1.8)
|
При решении задачи (2.1.1) элементы векторной последовательности 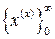 строятся, начиная с начального приближения x(0) Î En, согласно рекуррентному соотношению
строятся, начиная с начального приближения x(0) Î En, согласно рекуррентному соотношению
x(k + 1) = x(k) + aks(k), k = 0, 1, 2, …, (2.1.9)
где s(k) Î En – вектор, указывающий направление движения из точки x(k)
в точку x(k + 1). Вектор s(k) выбирается таким образом, чтобы обеспечить выполнение условия
f(x(k + 1)) < f(x(k)). (2.1.10)
В этом случае его принято называть направлением спуска.
ak – число, указывающее длину шага в направлении s(k). Длина шага определяется из условия
f(x(k) + aks(k)) = min f(x(k) + as(k)), (2.1.11)
a Î E1
т. е. в результате решения задачи одномерной оптимизации (см. гл. 1). В тех случаях, когда решение задачи (2.1.11) оказывается довольно трудным или нецелесообразным, выбор ak на k-м шаге процесса можно осуществлять, исходя из более слабого условия, согласно которому достаточно выполнения соотношения
f(x(k + 1)) < f(x(k)). (2.1.12)
В качестве условий (критериев) идентификации оптимального решения задачи (2.1.1) могут использоваться необходимые и достаточные условия экстремума функции нескольких переменных.
Приведем еще несколько определений.
Дата добавления: 2021-07-22; просмотров: 590;











