Метод золотого сечения

Это один из наиболее эффективных методов нулевого порядка, использующихся для решения задачи (1.1.1).

Опуская этап отделения (локализации) положения локального минимума функции f(x), перейдем к этапу уточнения положения этого минимума. Начнем с исходного интервала неопределенности D₀ = (a, b), содержащего х^* – искомую точку локального минимума унимодальной на интервале D₀ функции f(x). Как и в методе половинного деления, последовательное уточнение положения точки х^* представляет собой итерационный процесс. На каждом шаге этого процесса строится новый интервал неопределенности; его длина меньше длины текущего интервала, в который он входит. В результате построения получаем последовательность вложенных интервалов неопределенности D_i, i = 0, 2, 3, …, k, …:

D₀ = (a, b) É D₁ = (a⁽¹⁾, b⁽¹⁾) É … É D_k = (a^(k), b^(k)) É …

При этом если исходный интервал D₀ содержит искомую точку х^*, то ее будут содержать и все остальные интервалы последовательности.

Пусть L_i – длина i-го интервала неопределенности, i = 0, 2, 3, …, k, … Так же как и при использовании метода половинного деления, для анализа текущего интервала неопределенности D_i на i-м шаге процесса будем выбирать внутри этого интервала две пробные точки, расположенные симметрично относительно его середины. Однако в отличие от метода половинного деления потребуем, чтобы для строящейся последовательности вложенных интервалов выполнялись следующие условия:

– длина каждого интервала должна равняться сумме длин двух последующих интервалов этой последовательности:

L_i = L_{i + 1} + L_{i + 2}, i = 0, 1, 2, …; (1.3.1)

– отношение длины любого интервала последовательности к длине предыдущего интервала должно оставаться постоянным и равным некоторому числу l (0 < l < 1):

L_{i + 1} / L_i = L_{i + 2} / L_{i + 1} = l, i = 0, 1, 2, … (1.3.2)

Последнее условие часто называют правилом "золотого сечения".

Из совместного решения уравнений (1.3.1) и (1.3.2) находим

l = (-1+Ö(5))/2»0,618

Итак, согласно методу золотого сечения на i-м шаге пробные точки располагаются на расстоянии » 0,382L_i от концов текущего интервала
неопределенности D_i. При i = 0 потребуется введение сразу двух пробных точек для интервала D₀; при всех i > 1 достаточно будет ввести лишь одну новую точку в интервал D_i, так как одна из пробных точек, использовавшихся для интервала D_{i – 1}, останется таковой и для D_i. Таким образом,
за k-шагов процесса потребуется лишь k + 1 вычислений функции. Длина интервала неопределенности D_k на k-м шаге метода будет определяться по формуле

L_k = l^k L₀, k = 0, 1, 2, …

В итоге для уменьшения интервала неопределенности не менее чем в 100 раз потребуется сделать 10 шагов и, следовательно, 11 вычислений значений функции f(x), что лучше, чем при использовании метода половинного деления, где для этого потребовалось произвести 14 вычислений.

Пусть функция f(x) является унимодальной на интервале (a, b)
и задано достаточно малое число d > 0 – требуемая точность определения
точки искомого минимума х^* Î (a, b) данной функции. Тогда метод золотого сечения можно записать в виде следующего алгоритма:

1. Задать функцию f(x) и числа a, b, t » 0.618, d > 0;

2. Если b – a £ 2d Þ перейти к выполнению п. 11.

3. Вычислить с =t (b – a).

4. Вычислить x₁ =b – с; x₂ = a + с.

5. Вычислить значения f(x₁) и f(x₂).

6. Если f(x₁) > f(x₂) положить a:= x₁.

Иначе перейти к выполнению п. 8.

7. Если (b – a) £ 2d перейти к выполнению п. 11.

Иначе положить x₁ = x₂; f(x₁):= f(x₂).

Вычислить с =t (b – a), x₂ = a + с, f(x₂). Перейти к выполнению п. 6.

8. Если f(x₁) < f(x₂) положить b:= x₂.

Иначе перейти к выполнению п. 10.

9. Если (b – a) £ 2d перейти к выполнению п. 11.

Иначе положить x₂ = x₁; f(x₂)= f(x₁).

Вычислить с =t (b – a), x₁ =b – с, f(x₁). Перейти к выполнению п. 6.

10. Положить a:= x₁; b:= x₂.

Иначе перейти к выполнению п. 2.

11. Положить х^* =(a + b)/2. Процесс завершен.

Работу метода золотого сечения удобно отображать в таблице, аналогичной предложенной для метода половинного деления (см. табл. 1.2.1).

В заключение дадим общую характеристику метода золотого сечения для решения задачи (1.1.1), которая во многом сходна с характеристикой метода половинного деления:

– всегда сходится к решению задачи (1.1.1);

– скорость сходимости линейная. На каждом шаге длина интервала неопределенности уменьшается в l » 0.618 раз. После k-го шага процесса она составит L_k = l^kL₀. Нетрудно подсчитать количество итераций, необходимых для уменьшения исходного интервала неопределенности в заданное количество раз. Например, чтобы уменьшить ее не менее чем в 100 раз, потребуется 10 итераций;

– на каждом шаге (кроме нулевого) требуется вычисление значений функции f(x) в одной из точек: х₁ или х₂. Эти точки расположены симметрично относительно центра текущего интервала неопределенности на расстоянии » 0.236(b – a) друг от друга, где (a, b) – текущий интервал неопределенности. На нулевом шаге значение функции f(x) необходимо вычислить в обеих точках.

Общее количество итераций метода золотого сечения, необходимое для достижения заданной точности решения будет примерно в 1,4 раза больше, чем при использовании метода половинного деления. Тем не менее, метод золотого сечения оказывается эффективнее за счет меньшего совокупного количества вычисляемых при этом значений функции f(x).

Метод Ньютона

Рассмотрим теперь применение метода Ньютона для решения задачи (1.1.1). Его можно отнести к методам второго порядка, поэтому одним из условий его использования является принадлежность функции f(x) к классу дважды дифференцируемых функций.

Метод представляет собой многошаговый итерационный процесс поиска решения в общем случае нелинейного уравнения

f^¢(x) = 0. (1.4.1)

Как уже было отмечено, решение уравнения (1.4.1) соответствует стационарной точке функции f(x), следовательно, в этой точке выполнены необходимые условия экстремума. Для того чтобы решение (1.4.1) соответствовало точке локального минимума функции, в этой точке должны быть выполнены соответствующие достаточные условия (см. § 1.1).

В процессе работы метода Ньютона начиная с точки х⁽⁰⁾ начального приближения к решению (1.4.1) строится 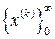(в общем случае бесконечная последовательность точек х⁽⁰⁾, х⁽¹⁾, х⁽²⁾, …, х^(k)…) посредством вычисления каждого очередного элемента последовательности по формуле

x^{(k +1)} = х^(k) – f^¢(х^(k)) / f^¢¢(х^(k)), k = 0, 1, 2, … (1.4.2)

Для того чтобы метод сходился, в некоторой окрестности искомой точки должны быть выполнены требования, предъявляемые к свойствам функции f(x), а также к выбору начального приближения х⁽⁰⁾.
С практической точки зрения рекомендуется выбирать х⁽⁰⁾ достаточно близко к х^* – искомому решению. Для работы метода необходимо также, чтобы f^¢¢(х^(k)) ¹ 0, "k.

Условия сходимости метода Ньютона приведены в литературе по вычислительной математике.

Рекуррентное соотношение (1.4.2) получено на основании следующих соображений.

В общем случае нелинейная функция f^¢(x) аппроксимируется
в окрестности точки х^(k) линейной функцией j(x):

j(x) = f ^¢(х^(k)) + f ^¢¢(х^(k))(x – х^(k)). (1.4.3)

Затем ищется решение линейного уравнения

j(x) = f^¢(х^(k)) + f ^¢¢(х^(k))(x – х^(k)) = 0, (1.4.4)

которое может быть записано в виде

x = х^(k) – f^¢(х^(k))/f^¢¢(х^(k)). (1.4.5)

Теперь рекуррентное соотношение (1.4.2) можно получить из (1.4.5), если в правой части последнего вместо x записать x^{(k + 1)}.

Другими словами, на каждом шаге метода Ньютона вместо решения нелинейного в общем случае уравнения (1.4.1) ищется решение линейного уравнения (1.4.4), которое и принимается за очередное приближение к решению задачи (1.4.1). Нетрудно увидеть, что по сути речь идет об использовании метода касательных (метода Ньютона – Рафсона) при решении нелинейного уравнения (1.4.1). Применительно к минимизируемой функции f(х) на каждом шаге метода Ньютона осуществляется ее квадратическая аппроксимация и поиск минимума соответствующей квадратической функции.

Запишем метод Ньютона в более формализованном виде. Пусть f(x) – дважды дифференцируемая функция в некоторой области W Ì X, в которой выполнены условия сходимости метода Ньютона и х⁽⁰⁾ Î W; достаточно малое число d > 0 задает точность отделения от нуля значений f^¢(x). Тогда метод Ньютона для решения задачи (1.1.1) можно записать в виде следующего алгоритма.

1. Задать х⁽⁰⁾ Î W, d > 0; положить k = 0.

2. Вычислить f ^¢(х^(k)), f ^¢¢(х^(k)).

3. Если÷f ^¢(х^(k))ç £ d, то перейти к выполнению п. 6.

4. Вычислить x^{(k + 1)} = х^(k) – f ^¢(х^(k)) / f ^¢¢(х^(k)).

5. Положить k: = k + 1. Перейти к выполнению п. 2.

6. Положить х^*: = х^(k). Процесс завершен.

Критерием окончания работы данного алгоритма является близость
к нулю значения f ^¢(х^(k)). Наряду с этим критерием могут быть использованы и другие (это определяется внешними требованиями к работе алгоритма и характером задачи), например близость к нулю разности двух последних членов последовательности .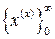

Результаты работы метода Ньютона удобно отображать в табличной форме (табл. 1.4.1).

Таблица 1.4.1

Отметим характерные особенности метода Ньютона:

– применяется только к дважды (и более) дифференцируемым функциям;

– требует вычисления на каждой итерации производных первого
и второго порядков минимизируемой функции f(x). Отсюда следует,
что метод Ньютона характеризуется сравнительно большой трудоемкостью выполнения каждой итерации.

– в процессе работы строится последовательность точек х⁽⁰⁾, х⁽¹⁾,
х⁽²⁾,…, х^(k), …, которая при выполнении условий сходимости будет сходиться к точке х^* – локальному минимуму минимизируемой функции f(x);

– не обладает так называемым свойством глобальной сходимости. Это означает, что сходимость метода Ньютона гарантируется только при хорошо выбранном начальном приближении х⁽⁰⁾. Поэтому метод Ньютона часто применяют в комбинации с другими методами, которые позволяют построить достаточно хорошее начальное приближение.

– при выполнении условий сходимости скорость сходимости метода квадратическая;

– для квадратических функций решение находится за один шаг.

Метод Ньютона достаточно часто используется в практических приложениях, что объясняется прежде всего его более быстрой сходимостью к решению по сравнению с рассмотренными ранее методами. Однако присущие методу Ньютона недостатки, а именно отсутствие свойства глобальной сходимости и большая трудоемкость вычислительных операций, выполняемых на каждой итерации, зачастую снижают его практическую значимость. Поэтому существуют так называемые квазиньютоновские методы, являющиеся модификациями классического метода Ньютона. Они позволяют при сохранении достаточно высокой скорости сходимости снизить влияние отрицательных свойств данного метода. Модификации метода Ньютона рассмотрены во многих руководствах по изучению вычислительной математики.