Коммутативный ключ КМОП
Для построения элементов с Z-состоянием используется коммутативный ключ, схема которого приведена на рис. 1.23, а поведение описано таблицей 1.11.
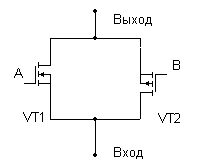
Рис. 1.23 Коммутативный ключ
Таблица 1.11
Состояния коммутативного ключа
| A | B | VT1 | VT2 | Примечание |
| закрыт | открыт | Не используется | ||
| закрыт | закрыт | Z-состояние | ||
| открыт | открыт | Коммутация | ||
| открыт | закрыт | Не используется |
Как видно из табл. 1.11 сочетание сигналов A = B не используется (первая и четвертая строка таблицы). Обязательным условием является
A &B =0. Рабочими являются две ситуации:
A = 0, B = 1 – оба транзистора закрыты, ключ разомкнут;
A = 1, B = 0 – оба транзистора открыты, ключ замкнут
Основным достоинством такого ключа является возможность коммутации сигналов в двух направлениях, т.е. вход и выход можно менять местами, а значит такой ключ способен коммутировать не только цифровые, но и аналоговые сигналы. Переходное сопротивление ключа зависит от напряжения питания и лежит в пределах от десятков до сотен Ом.
Типичным представителем является четырехканальный двунаправленный коммутативный ключ К561КТ3, в котором каждый канал независим от соседних и способен коммутировать цифровые и аналоговые сигналы с током коммутации до 10 мА.
Код Грея
Код Грея непозиционный, т.е. веса его разрядов не определяются занимаемыми ими местами, как в обычном двоичном коде, который относится к классу позиционных.
| десятичный | двоичный позиционный | код Грея непозиционный |
Каждый n-ый считая слева, разряд числа в коде Грея равен сумме по модулю 2 n-го и (n-1)-го слева разрядов того же числа, представленного позиционным кодом.
Помним, что:
Сумма по модулю 2 это Y = 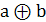 =
= 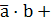
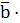
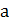 , потому:
, потому:
0 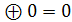
0 ⊕ 1 = 1
1 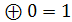
1 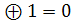
Замечательным свойством кода Грея является то, что при переходе между любыми соседними числами изменяется значение всегда только одного разряда, а у двоичного кода на все сочетания эта величина колеблется от 1 до n, где n – число разрядов, что приводит к ошибкам неоднозначности при считывании кодов.
Преобразование кода Грея в двоичный позиционный можно выполнить по схеме, приведенной на рис. 1.24, а обратное преобразование по схеме рис. 1.25.
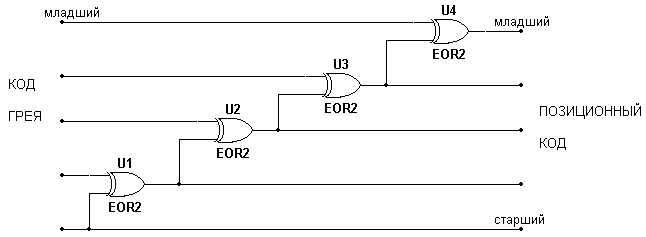
Рис. 1.24 Преобразователь кода Грея в двоичный
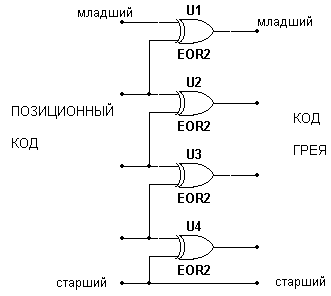
Рис. 1.25 Преобразователь двоичного кода в код Грея
Дата добавления: 2017-05-02; просмотров: 2613;











