Связи, классификация связей, число степеней свободы.

Положение системы N материальных точек определяется сово­купностью 3N декартовых координат: 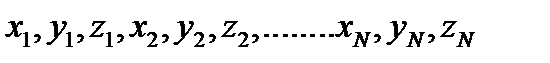этих точек. Положение твердого тела задается тремя коор­динатами 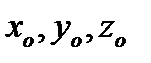одной из его точек, принятой за полюс, и тремя эйлеровымигпнп углами 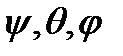. Если система состоит из ряда твердых тел, то для определения положения такой системы в пространстве достаточно задать координаты полюсов и значения эйлеровых углов для каждого из тел. Положение твердых тел можно задавать не только эйлеровыми углами, но и другими, играю­щими аналогичную роль параметрами. Таким образом, для опреде­ления положения материальной системы в пространстве применяют самые разнообразные приемы. Любая совокупность параметров, достаточная для определения положения системы в пространстве, называется обобщенными координатами системы. При этом не предрешается вопрос о том, все ли координаты необходимы для указанной цели, нельзя ли определить положение системы при по­мощи только части этих параметров или вообще меньшего числа параметров. Вообще если положение движущейся системы N материальных точек 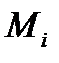с прямоугольными координатами ( 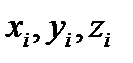) в любой мо­мент времени может быть задано при помощи какой-нибудь сово­купности обобщенных координат ( 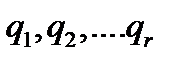), то между первой и второй совокупностями должны существовать соотношения вида:

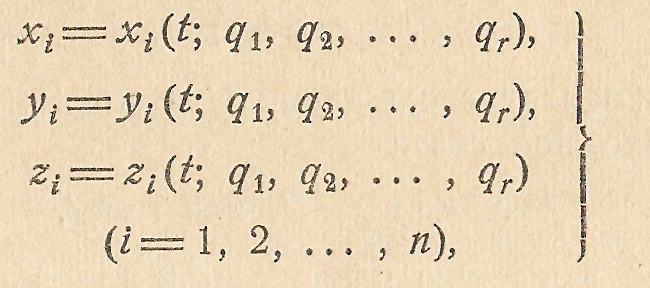
содержащие в общем случае явно время. Если материальная система несвободна, то обобщенные коор­динаты 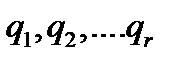так же как и их производные по времени - обобщенные скорости 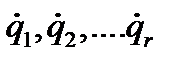подчиняются ограничительным условиям, которые мы называем связями. Аналитически связи выра­жаются равенствами, заключающими время, координаты и их про­изводные, и иногда сопровождаемые знаками неравенств; последние указывают на возможность прекращения действия связей. Остано­вимся на случае связей, выражаемых равенствами. Связи, выражаемые аналитически уравнениями вида

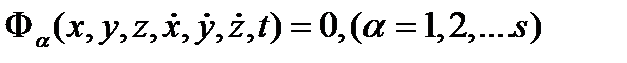(4.1)

носят общее наименование кинематических; обобщенные скорости в соотношение (4.1), как правило, входят линейно.

Если время не входит явно в уравнения связей, то такие связи называют стационарными, в противном случае - нестационарными.

Кинематические связи, уравнения которых не содержат обобщен­ных скоростей или путем интегрирования могут быть к такому виду приведены, называют голономными или интегрируемыми, в против­ном случае - неголономными или неинтегрируемыми.

Голономные связи накладывают ограничения на координаты то­чек системы, т.е. на ее положение в пространстве. Вместе с тем, будучи продифференцированы по времени, уравнения голономных связей представляют ограничения, накладываемые на скорости точек системы. В противоположность этому неголономные связи ограничи­вают только скорости точек системы, так как уравнения связей не могут быть проинтегрированы и, следовательно, не существует конечных соотношений между координатами, соответствующих неголономным связям. Примером голономной нестационарной связи может служить математический маятник переменной длины

.

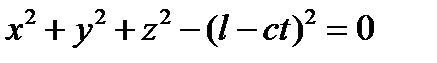Если уравнение связи задано неравенствами, то такая связь называется односторонней (если знак равенства – то двухсторонней).

Чем больше число условий, налагаемых связями на бесконечно малые перемещения системы, тем меньше произвола остается в опре­делении возможных перемещений. Это обстоятельство характеризуют числом степеней свободы системы, которое определяется как число независимых, допускающих выбор по произволу, координат системы. Так для трёх свободных точек будем иметь 9 независимых координат 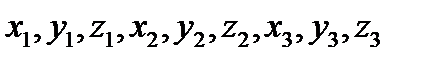, или 9 степеней свободы. Но если все точки соеденены жесткими стержнями, то имеются три уравнения связей

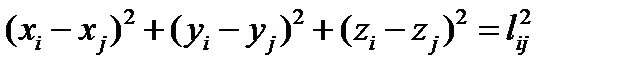
(расстояния между точками остаются неизменными), т.е. теперь это твёрдое тело и для определения его движения необходимо задать шесть параметров. Действительно, из девяти параметров независимыми являются 9-3=6 параметров. Это правило можно распространить для любого числа обобщённых координат при наличии голономных связей. В случае систем, подчиненных голономным связям, число степеней свободы совпадает с числом независимых обобщенных координат. Так, например, если система, состоящая из N точек, подчинена s голономным связям, то число степеней свободы такой системы согласно будет совпадать с числом независимых коор­динат k=3N-s. Точка, вынужденная двигаться по заданной поверхности, будет иметь две степени свободы; точка, движущаяся по заданной пространственной кривой, будет, иметь одну степень свободы и т. д. В тех случаях, когда положение системы определяется 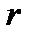обоб­щенными координатами 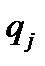,(j= 1, 2,..., 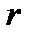), не являющимися, вообще говоря, независимыми, а подчиненными s голономным связям, число степеней свободы системы будет равно k = r-s, т. е. опять равно числу независимых обобщенных координат системы. Так, свободное твердое тело (r = 6, s = 0) имеет шесть степе­ней свободы, тело, вращающееся вокруг неподвижного центра, — три степени свободы, в плоском движении — также три степени свободы. Система с 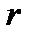обобщенными координатами, подчиненная s голо­номным и s' неголономным связям, будет иметь число степеней свободы k=r-s-s', равное числу (r-s) независимых обобщенных координат, уменьшен­ному на число s' неголономных связей.