Особенности теории наземной фотограмметрии

В принципе для теории фотограмметрии безразлично как снимок расположен в пространстве. Но незначительные особенности при картографировании по наземным снимкам есть, и их следует рассмотреть.

Во-первых, несколько иначе вводится система координат на наземном снимке (Рис.44), но в основном путем использования координатных меток. Как следует из рисунка, оси на снимке обозначены буквами x и z. Это означает, что его элементами внутреннего ориентирования являются величины f, x_о и z_о.

За начало фотограмметрической системы координат чаще всего принимают центр проекции S, ось Z устанавливают отвесно, а оси X и Y – горизонтально. Угловыми элементами внешнего ориентирования снимка являются: j - угол между осью Y и проекцией главного луча на плоскость SXY (на рисунке он отрицательный); w - угол наклона главного луча; k - разворот снимка в своей плоскости, например, угол между главной горизонталью и осью x (на рис. 44 не показан).

При определении пространственных координат точки на снимке формулы (15) примут вид:

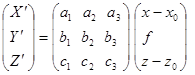
(112)

Направляющие косинусы матрицы A поворота в выше приведенной формуле получаются, как произведение A_fA_wA_k и могут быть вычислены по формулам:

При условии учета зависимостей (112) и (113), соотношения между координатами точек местности и снимка те же, что и для аэрофотоснимка, например, уравнения (25).

Если оси X иZ пространственной фотограмметрической системыкоординат параллельны соответствующим осям x и z снимка и координаты главной точки равны нулю, то, используя их, можно получить:

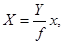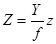
(114)

Значение координаты Y часто называют отстоянием. Из выше приведенной формулы следует, что отношение отстояния к фокусному расстоянию снимка является масштабом изображения.

Особенностью наземной фототопографии является и то, что при фотографировании объектов элементы внешнего ориентирования снимков устанавливаются с достаточно высокой точностью. Поэтому довольно часто координаты точек местности по паре снимков определяют путем решения прямой пространственной фотограмметрической засечки. При этом за начало фотограмметрической системы координат принимают центр проекции левого снимка пары, ось Y направляют вдоль проекции главного луча на горизонтальную плоскость, ось Z – отвесно, (система правая).

Угловые элементы внешнего ориентирования f, w и k, каждого из снимков стереопары являются и элементами самой пары. Но f,как правило, это угол в горизонтальной плоскости между проекцией на нее главного луча и перпендикуляром к базису фотографирования. Понятно, что при таком подходе линейные элементы внешнего ориентирования левого снимка равны нулю, а правого - это проекции базиса фотографирования на оси координат.

Отметим, что формулы прямой пространственной фотограмметрической засечки, установленные для пары аэрофотоснимков справедливы (с учетом выше приведенных замечаний) и для пары наземных снимков. Но после получения координат точек местности необходимо выполнять процесс внешнего ориентирования. В этом случае он проще, так как поворот следует выполнять только вокруг оси Z (снимок в процессе фотографирования устанавливается отвесно). Элементами внешнего ориентирования считают: геодезические координаты начала фотограмметрической системы координат X_s, Y_s и Z_s (левого центра проекции); дирекционный угол a главного луча (или базиса фотографирования a_b); поправку DZ_r за кривизну Земли и вертикальную рефракцию. Формулы преобразования в этом случае имеют вид: