Вычислительные методы линейной алгебры
Вычислительные методы линейной алгебры включают в себя решение следующих задач:
1) Решение систем линейных алгебраических уравнений (СЛАУ).
2) Вычисление определителей квадратной матрицы А.
3) Для данной квадратной матрицы А вычисление обратной А-1.
4) Определение собственных значений и собственных векторов квадратной матрицы А.
3.1. Нормы векторов и матриц
При решении многих прикладных задач весьма полезным являются понятия нормы векторов и нормы матриц.
Определение 3.1. Нормой вектора 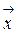 называется неотрицательное число, которое обозначается символом ||
называется неотрицательное число, которое обозначается символом ||  || и удовлетворяет следующим условиям:
|| и удовлетворяет следующим условиям:
1) ||  || > 0 при
|| > 0 при 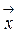 ¹
¹ 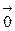 и ||
и || 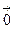 || = 0;
|| = 0;
2) || 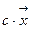 || = | c |×||
|| = | c |×||  || при любом числовом множителе;
|| при любом числовом множителе;
3. || 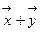 || ≤ ||
|| ≤ ||  || + ||
|| + || 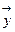 ||. Это соотношение называют неравенством треугольника.
||. Это соотношение называют неравенством треугольника.
Норму вектора можно ввести различными способами. Наиболее часто для векторов n-мерного арифметического пространства
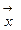 = (x1, x2, ..., xn)T используются следующие нормы:
= (x1, x2, ..., xn)T используются следующие нормы:
1) ||  ||1 =
||1 = 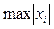 , i = 1, 2, ..., n (3.1)
, i = 1, 2, ..., n (3.1)
(называется кубической);
2) ||  ||2 =
||2 = 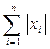 (3.2)
(3.2)
(называется октаэдрической);
3) ||  ||3 =
||3 = 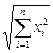 =
= 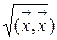 (3.3)
(3.3)
(называется сферической, порождена скалярным произведением и определяет длину вектора  ).
).
Норма (3.3) порождена скалярным произведением которое выражается формулой: 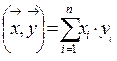 .
.
Для скалярного произведения векторов справедливы соотношения:
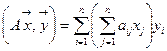 =
= 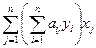 =
= 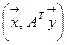 .
.
Если A симметричная матрица, то 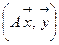 =
= 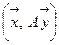 .
.
Определение 3.2. Если в пространстве векторов введена норма ||  ||, то согласованной с ней нормой в пространстве матриц называют норму
||, то согласованной с ней нормой в пространстве матриц называют норму
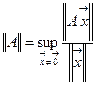 . (3.4)
. (3.4)
Согласованные с нормами векторов (3.1)-(3.3) нормы матриц определяются формулами
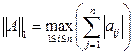 , (3.5)
, (3.5)
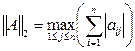 , (3.6)
, (3.6)
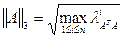 . (3.7)
. (3.7)
В формуле (3.7) 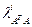 – собственные значения матрицы ATA, которая является симметрической.
– собственные значения матрицы ATA, которая является симметрической.
Формула (3.7) следует из того, что для симметрической матрицы B можно доказать справедливость соотношения:
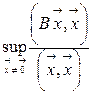 =
= 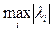 , (3.8)
, (3.8)
где li – собственные значения матрицы B.
Определение 3.3. Две нормы ||  ||α и ||
||α и ||  ||β называются эквивалентными, если существуют такие постоянные γ1 и γ2, что для всех векторов
||β называются эквивалентными, если существуют такие постоянные γ1 и γ2, что для всех векторов 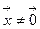 справедливы соотношения:
справедливы соотношения:
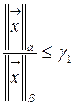 , и
, и 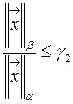 .
.
Нормы ||  ||1, ||
||1, ||  ||2 и ||
||2 и ||  ||3 эквивалентны между собой, так как выполнятся неравенства
||3 эквивалентны между собой, так как выполнятся неравенства
||  ||1 ≤ ||
||1 ≤ ||  ||3 ≤ ||
||3 ≤ ||  ||2 ≤ n×||
||2 ≤ n×||  ||1.
||1.
Определение 3.4. Будем говорить, что последовательность векторов 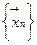 сходится к вектору
сходится к вектору  по данной норме ||
по данной норме ||  ||, если выполняется соотношение
||, если выполняется соотношение 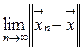 = 0.
= 0.
Из эквивалентности норм ||  ||1, ||
||1, ||  ||2 и ||
||2 и ||  ||3 следует, что если последовательность векторов сходится по одной из этих норм, то она сходится и по остальным нормам.
||3 следует, что если последовательность векторов сходится по одной из этих норм, то она сходится и по остальным нормам.
Договоримся в дальнейшем под нормой ||  || подразумевать одну из указанных выше норм, а при необходимости конкретизировать, какую именно.
|| подразумевать одну из указанных выше норм, а при необходимости конкретизировать, какую именно.
При этом под нормой матрицы будем понимать норму, согласованную с нормой матрицы.
3.2. Решение систем линейных алгебраических уравнений (СЛАУ)
Теоретические условия существования и единственности решения систем линейных уравнений известны – главный определитель не должен быть равен нулю. Тогда решение можно найти по правилу Крамера, или методом исключения неизвестныхГаусса. Метод Гаусса и правило Крамера относятся к прямым методам решения систем линейных алгебраических уравнений. Они позволяют за конечное число действий получить точное решение системы, при условии, что все действия выполняются точно, без округления. Но на практике, при больших порядках системы, правило Крамера требует слишком много времени для вычисления определителей. Если определители вычислять формально по определению как сумму п!слагаемых, то число операций имеет порядок п!п.Правило Крамера используется чаще для теоретических исследований, а на практике почти не применяется.
Метод исключения неизвестных Гаусса для решения систем линейных уравнений более эффективен, чем правило Крамера. Более того, он также эффективен при вычислении определителя и обратной матрицы.
При большом числе неизвестных иногда оказывается, что выгоднее решать систему уравнений методом итераций, который дает приближенное решение системы.
а) Метод Гаусса для решения систем линейных уравнений
Пусть требуется решить систему п линейных алгебраических уравнений с п неизвестными:
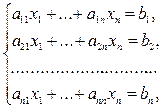 (3.9)
(3.9)
Прямой ходметода Гаусса преобразует систему (3.9) к треугольному виду исключением соответствующих неизвестных. Пусть a11 ¹ 0 . Первый шаг заключается в исключении переменной x1с помощью первого уравнения из остальных уравнений. Разделим первое уравнение на a11:
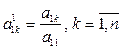 ;
; 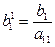 . (3.10)
. (3.10)
Затем от второго уравнения вычтем первое уравнение, умноженное на a21. В результате, на месте второго уравнения получим уравнение, не содержащее х1. Чтобы исключить х1 из третьего уравнения, вычтем из первое уравнение, умноженное на a31. Аналогично исключаем х1из четвертого и последующих уравнений. Для исключения х1из i-го уравнения (i = 2, 3, ... , п)применим формулы
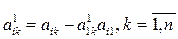 ;
; 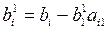 . (3.11)
. (3.11)
В результате этих вычислений получим систему вида
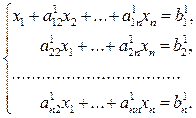 (3.12)
(3.12)
На втором шаге исключаем переменную х2с помощью второго уравнения из третьего и последующих уравнений. Предположим, что 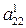 ¹ 0. Разделим второе уравнение на
¹ 0. Разделим второе уравнение на 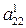 :
:
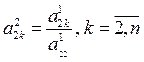 ;
; 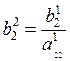 . (3.13)
. (3.13)
Затем в системе (3.12) с помощью второй строки исключим
х2 из i-го уравнения (i = 3, 4, ... , n), применяя формулы:
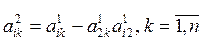 ;
; 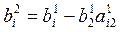 . (3.14)
. (3.14)
Система (3.12) преобразуется к следующему виду:
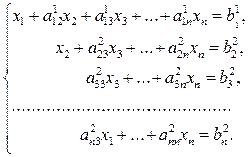 (3.15)
(3.15)
1. В общем случае на шаге т для т = 1, 2,..., n - 1,
делим сначала т-е уравнение на 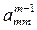 :
:
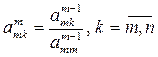 ;
; 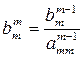 , (3.16)
, (3.16)
а затем исключаем переменную xm c помощью m-го уравнения из i-го, где
i = m +1,..., n:
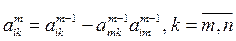 ;
; 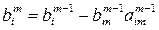 . (3.17)
. (3.17)
Здесь предполагается, что на каждом шаге выполняется условие 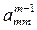 ¹ 0.
¹ 0.
В результате (n - 1)-го шага система (3.9) приобретает вид
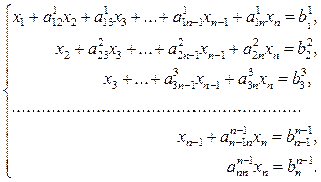 (3.18)
(3.18)
2. Обратный ход метода Гаусса вычисляет неизвестные xi в обратном порядке. Из последнего уравнения в (3.18) находим
хп = 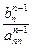 (3.19)
(3.19)
Неизвестные xi определяем по следующим формулам:
xi = 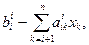 i = n - 1,n - 2,..., 1.(3.20)
i = n - 1,n - 2,..., 1.(3.20)
Метод Гаусса предполагает, что на т-мшаге выполняется условие 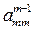 ¹ 0. Если это условие не выполняется, то алгоритм перестанет работать, так как столкнется с делением на 0. Кроме этого, в случае выполнения условия
¹ 0. Если это условие не выполняется, то алгоритм перестанет работать, так как столкнется с делением на 0. Кроме этого, в случае выполнения условия 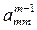 ¹ 0, может возникнуть ситуация, когда ведущий элемент
¹ 0, может возникнуть ситуация, когда ведущий элемент 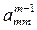 близок к нулю, что также может привести к неприятностям в виде больших погрешностей.
близок к нулю, что также может привести к неприятностям в виде больших погрешностей.
Чтобы избежать этих трудностей, применяют метод Гаусса с выбором главного элемента.Одним из вариантов этого метода является метод Гаусса с выбором главного элемента по столбцам.В качестве ведущего элемента на каждом шаге выбирают наибольший по модулю элемент столбца и переставляют соответствующую строку с другой строкой так, чтобы найденный элемент стал диагональным, затем исключают соответствующую переменную. Так как при этих перестановках переменные в уравнениях остаются на своих местах, решение преобразованной системы совпадает с решением исходной системы уравнений.
Метод Гаусса с выбором главного элемента по столбцамотличается от алгоритма (3.16) – (3.20) только тем, что перед преобразованием (3.16) нужно выполнить поиск максимального по модулю элемента в т-мстолбце и переставить строки системы уравнений так, чтобы максимальный элемент стал диагональным элементом матрицы коэффициентов.
б) Алгоритм метода Гаусса с выбором главного элемента
По столбцам
1. Для т = 1, 2, ... , п - 1 выполним преобразования: Найдем максимальный по абсолютной величине элемент в т-м столбце. Пусть это будет элемент aim.Если i ¹ т, то меняем местами i-ю и т-юстроки:
r = 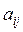 ,
, 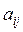 =
= 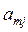 ,
, 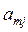 = r , j = 1, ... , п;
= r , j = 1, ... , п;
r = bi, bi = bт, bт = r.
Элементы матрицы и вектора-столбца свободных членов после преобразования на т-м шаге обозначим 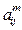 ,
, 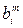 , причем
, причем 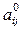 =
= 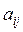 ,
, 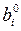 = bi.
= bi.
Делим т-е уравнение на ведущий элемент 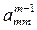 :
:
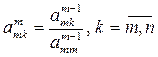 ;
; 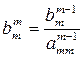 ,
,
затем исключаем переменную хт с помощью m-го уравнения из i-го, где
i = т + 1,..., п:
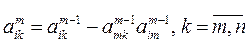 ;
; 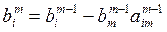 .
.
2.Вычисляем неизвестные xi в обратном порядке:
хп = 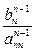 ; xi =
; xi = 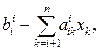 i = n - 1,n - 2,..., 1.
i = n - 1,n - 2,..., 1.
Приведенный вариант метода Гаусса дает решение и тогда, когда обычный метод Гаусса перестает работать из-за деления на 0.
При реализации метода Гаусса на каком-либо языке программирования удобно использовать исходные матрицу a и вектор bдля хранения промежуточных результатов преобразований. Приведенные формулы преобразований записываются как операторы присваивания, т. е. имена переменных aij и bi записываются без верхних индексов.
В методе Гаусса с выбором главного элемента по строкам на каждом шаге выбирают наибольший по модулю элемент строки и переставляют столбцы так, чтобы ведущий элемент находился на диагонали. В этом варианте в уравнениях неизвестные переменные меняются местами и в алгоритме необходимо думать о том, чтобы запомнить эти перестановки.
В общем случае метода Гаусса с выбором главного элемента на шаге т ищется максимальный по модулю элемент во всей матрице коэффициентов и производится перестановка строк и столбцов так, чтобы этот элемент стал диагональным.
Отметим, что последний вариант с выбором главного элемента считается лучшим.
Общее число операций для решения системы уравнений методом Гаусса составляет приблизительно 2n3/3 + 2n2, при этом большая часть, т. е. 2п3/3, операций приходится на прямой ход.
в) Итерационный метод
Запишем систему уравнений (3.9) в виде
Ах = b,(3.21)
где А – матрица коэффициентов; b– вектор правых частей системы.
Преобразуем (3.21) к виду, удобному для итераций:
х = Вх + с. (3.22)
Тогда метод простой итерации определяется формулой:
xk+1 = Bxk + c, k = 0, 1, ... , (3.23)
где начальное приближение x0 задано.
В качестве критерия сходимости метода итераций обычно применяют условие
||xk+1 - xk|| £ ε.
Сформулируем теоремы об условиях сходимости метода простых итераций.
Теорема 3.1 (достаточное условие сходимости).Если ||В|| < 1, то система (3.21) имеет единственное решение, а итерационный метод (3.23) сходится к решению со скоростью геометрической прогрессии.
Теорема 3.2. (необходимое и достаточное условие сходимости).Пусть система (3.22) имеет единственное решение. Итерационный процесс (3.23) сходится к решению системы (3.22) тогда и только тогда, когда все собственные значения матрицы В по модулю меньше единицы.
Теоремы 3.1 и 3.2 не дают способов преобразования произвольной системы линейных уравнений к виду (3.22) так, чтобы метод итераций (3.23) при этом сходился к решению. Эти теоремы имеют важное теоретическое значение. На практике для проверки условия сходимости метода итераций более полезна теорема 3.1, а теорему 3.2 удается использовать тогда, когда собственные значения матрицы В известны. Задача определения собственных значений матрицы в общем случае сложнее, чем задача решения системы линейных уравнений.
Для преобразования системы уравнений к виду, удобному для итераций, можно умножить систему (3.21) на матрицу D = А-1- ε, где ε – произвольная матрица. Тогда система примет вид (3.22)
х= Вх + с, В = εА, с = Db (3.24)
и матрица В будет удовлетворять теореме 3.1, если выбрать элементы матрицы ε достаточно малыми по модулю. Однако этот прием не выгоден, так как для вычисления обратной матрицы А-1необходимо выполнить не меньше операций, чем при решении самой системы.
При небольшом числе уравнений систему иногда удается привести к виду, удобному для итераций, с помощью нескольких преобразований.
Далее будут рассмотрены разностные методы решения краевых задач для обыкновенных дифференциальных уравнений и уравнений в частных производных, которые приводят к решению систем линейных уравнений с большим числом неизвестных. Учитывая специфику таких систем, часто удается построить эффективные итерационные методы их решения.
г) Метод Зейделя
Пусть требуется решить систему уравнений (3.1):
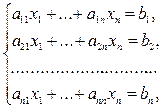 (3.25)
(3.25)
Выразим из первого уравнения переменную х1 из второго – х2и т. д.:
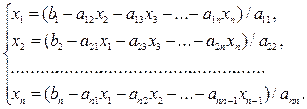
Пусть k-e приближение к решению обозначено как хk = 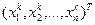 . Подставим его в правую часть полученной системы и выразим следующее приближение xk+1=
. Подставим его в правую часть полученной системы и выразим следующее приближение xk+1= 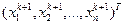 .В отличие от метода итераций, метод
.В отличие от метода итераций, метод
Зейделя использует при вычислении 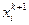 уже найденные компоненты
уже найденные компоненты 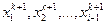 вектора хk+1.
вектора хk+1.
Расчетные формулы метода Зейделя можно записать в виде
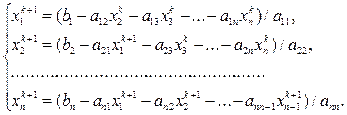 (3.26)
(3.26)
Теорема 3.3(достаточные условия сходимости).Пусть при всех i для коэффициентов системы уравнений (3.25) выполняются условия
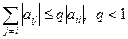 . (3.27)
. (3.27)
Тогда метод Зейделя сходится и выполняется неравенство
||xk+1 - xk||1 £ q||xk – x*||1 (3.28)
где х* – точное решение системы (3.25).
Если матрица А удовлетворяет условию (3.27), говорят, что А – матрица с диагональным преобладанием.
Теорема 3.4(достаточные условия сходимости).Пусть матрица А системы (3.1) – вещественная, симметричная и положительно определенная. Тогда метод Зейделя сходится.
3.3.Погрешность решения и обусловленность системы уравнений
Рассмотрим влияние погрешности правой части и свойств матрицы системы линейных уравнений на погрешность решения. Пусть правая часть системы задана приближенно, с погрешностью η:
Ах = b1,b1 = b + η.
Пусть х1 решение неточно заданной системы Ах = b1, х – решение точной системы Ах = b.Обозначим погрешность решения через r = х1 - х.Тогда можно запить Ах1= b1в виде А (х + r) = b + η,и Аr= η.
Определение 3.5. Мерой обусловленности системы называется число
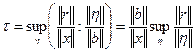 . (3.29)
. (3.29)
Мера обусловленности системы равна верхней грани отношения относительной погрешности решения к относительной погрешности правой части. Из формулы (3.29) следует неравенство
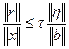 (3.30)
(3.30)
Если мера обусловленности системы принимает большое значение, это значит, что небольшая погрешность правой части может привести к большой погрешности решения, т. е. полученное приближенное решение окажется непригодным.
Учитывая, что r = А-1η,можно получить формулу вычисления меры обусловленности системы:
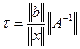 (3.31)
(3.31)
Определение 3.6. Мерой обусловленности матрицы А называется число
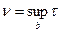 . (3.32)
. (3.32)
Для вычисления меры обусловленности матрицы можно с помощью (3.31) получить формулу
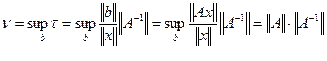 . (3.33)
. (3.33)
Учитывая (3.30), можно записать
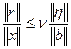
 (3.34)
(3.34)
Неравенство (3.34) связывает относительные погрешности правой части и решения системы через свойства матрицы системы.
Определение 3.7. Системы уравнений и матрицы называются плохо обусловленными,если их меры обусловленности принимают большие значения, и хорошо обусловленными,если меры обусловленности принимают малые значения.
Понятно, что при решении хорошо обусловленных систем малые погрешности правой части приводят к малым погрешностям решения, а плохо обусловленные системы уже нельзя решать обычными методами.
3.4. Вычисление определителя и обратной матрицы
Вычисление определителя матрицы является классическим примером задач, для решения которых важно найти эффективные алгоритмы.
При непосредственном раскрытии определителя квадратной матрицы
n-го порядка нужно найти сумму n! слагаемых, каждое из которых равно произведению n элементов матрицы, взятых по одному с каждого столбца и каждой строки, т. е. нужно выполнить порядка n!n операций. Число операций для вычисления определителя 100-го порядка приблизительно равно 100! × 100 = 100157,9 × 100. Такое число операций не способен выполнить за приемлемое время ни один из существующих суперкомпьютеров. Тем не менее современные компьютерные программы вычисления определителей справляются с матрицами и более высокого порядка, используя экономичные алгоритмы. Одним из таких алгоритмов является метод Гаусса.
Если матрица приведена к диагональному или треугольному виду, то ее определитель равен произведению диагональных элементов.
Для преобразования матрицы к треугольному виду можно применить метод Гаусса, который потребует порядка 2n3/3 операций.
Для n = 100 имеем 2n3/3 = 0,67 ×106. На 


 такой объем арифметических операций современный персональный компьютер тратит не более 1 с.
такой объем арифметических операций современный персональный компьютер тратит не более 1 с.
Если внимательно проанализировать метод Гаусса, то можно увидеть, что он фактически позволяет одновременно с приведением матрицы коэффициентов к треугольному виду, вычислить определитель этой матрицы. Действительно, определитель матрицы коэффициентов системы уравнений (3.18) равен произведению диагональных элементов, т. е. единице. С другой стороны, если к любой строке матрицы прибавить другую строку, умноженную на число, определитель не изменится. А если строку матрицы разделить на число, отличное от нуля, то определитель матрицы разделится на то же число. Отсюда следует, что в результате преобразований к виду (3.18), определитель матрицы коэффициентов системы уравнений (3.9) изменился на множитель, который равен произведению ведущих элементов, т. е. мы получаем формулу для вычисления определителя
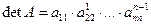 .
.
Метод Гаусса также эффективен и для вычисления обратной матрицы. Вычисление обратной матрицы можно рассматривать как частный случай решения совокупности систем линейных уравнений с одной и той же матрицей коэффициентов и разными правыми частями. В этом случае преобразования, которые применяются к столбцу правых частей системы, нужно применить к нескольким столбцам правых частей.
3.5. Собственные числа и собственные векторы матрицы
Приведем основные определения и теоремы, необходимые для решения практических задач вычисления собственных чисел и собственных векторов матриц.
Определение 3.8. Собственным числом (или собственным значением) квадратной матрицы А называется число λ, такое, что система уравнений
Ах = λх (3.35)
имеет ненулевое решение х. Это решение называется собственным вектором матрицы А,соответствующим собственному значению λ.
Собственный вектор определяется с точностью до постоянного множителя, если худовлетворяет (3.35), то и схтакже является решением (3.35).
Преобразуем систему (3.35) к виду (А - λЕ) х = 0, где Е – единичная матрица. Так как система линейных однородных уравнений имеет ненулевые решения лишь тогда, когда определитель матрицы равен нулю, получим уравнение для определения собственных значений
det(A – λE) = 0, (3.36)
которое называется характеристическим,или вековым, уравнением.
Если раскрыть определитель, то получим в левой части (3.36) многочлен n-й степени, корнями которого являются собственные значения матрицы А. На практике, при больших порядках п матрицы, задача раскрытия определителя (3.36) является сложной. Как известно из алгебры, многочлен n-й степени имеет п корней (действительных или комплексных), если кратные корни учитывать столько раз, какова их кратность.
Вычислить собственные значения матрицы в общем случае труднее, чем найти при известных собственных значениях соответствующие собственные векторы. В некоторых частных случаях собственные значения вычисляются легко. Например, если матрица диагональная или треугольная, определитель равен произведению диагональных элементов и поэтому собственные значения равны диагональным элементам. Нетрудно вычислить собственные значения для трехдиагональной матрицы, а также для почти треугольной матрицы.
Для диагональной матрицы собственному значению λi = aii отвечает единичный собственный вектор хi = (0, ... , 1, ... ,0)T, у которого i-якомпонента равна 1, а остальные компоненты 0.
Теорема 3.5. Собственные значения симметричной матрицы с действительными элементами действительны, а собственные векторы, соответствующие различным собственным значениям, взаимно ортогональны.
Теорема 3.6.Если λmin и λmах – наименьшее и наибольшее собственные значения действительной симметричной матрицы А, то для любого вектора хсправедливо неравенство
λmin(x, х)£(Ах, х)£ λmax(х, х).(3.37)
Определение 3.9.Действительная симметричная матрица А называется положительно определенной, если для любого вектора х¹0 выполняется условие
(Ах, х)> 0.(3.38)
Теорема 3.7.Действительная симметричная матрица А является положительно определенной тогда и только тогда, когда все ее собственные значения положительны.
Теорема 3.8(критерий Сильвестра).Для того чтобы действительная симметричная матрица А = (аij) была положительно определенной, необходимо и достаточно, чтобы все главные диагональные миноры ее определителя были положительны:
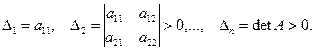 (3.39)
(3.39)
Теорема 3.9(теорема Перрона).Если все элементы квадратной матрицы положительны, то ее наибольшее по модулю собственное значение положительно и не является кратным, а соответствующий собственный вектор имеет положительные координаты.
Рассмотрим итерационный методопределения наибольшего по модулю собственного значения и соответствующего собственного вектора матрицы А,который запишем в виде следующего алгоритма.




 Алгоритм определения наибольшего по модулю собственного значения и соответствующего собственного вектора матрицы с положительными элементами:
Алгоритм определения наибольшего по модулю собственного значения и соответствующего собственного вектора матрицы с положительными элементами:
1) зададим начальное приближение х0к собственному вектору; k = 0;
2) вычислим следующие приближения хk+1 по формулам
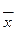 k+1 = Axk,
k+1 = Axk, 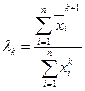 , xk+1 =
, xk+1 = 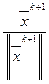 , k = k+1; (3.40)
, k = k+1; (3.40)
3) если |λk+1 - λk| ³ ε,переходим к п. 2, иначе – к п. 4;
4) конец.
Критерием для остановки итераций является условие |λk+1 - λk| < ε – заданная погрешность.
С помощью формулы (3.40) можно вычислить сначала k-юстепень матрицы А и умножить ее на вектор х0(см. пример 10), а для λk можно брать отношение ненулевой координаты вектора хk+1 к соответствующей координате
вектора хk, которая также не должна быть равной нулю. Так как заранее неизвестно, какие координаты собственного вектора не равны нулю, можно брать отношение сумм координат, если эта сумма не равна нулю.
3.6.Метод скалярных произведений
Рассмотрим метод скалярных произведений для определения наибольшего собственного значения и соответствующего собственного вектора действительной матрицы А.
Теорема 3.10.Транспонированная матрица АT имеет те же собственные значения, что и матрица А. Пусть λi и λk –различные собственные значения матрицы А (и транспонированной матрицы АT), хi – собственный вектор матрицы А, отвечающий собственному значению λi а yk – собственный вектор матрицы АT, отвечающий собственному значению λk.Тогда векторы хi и уk – ортогональны.
Пусть требуется вычислить наибольшее собственное значение и соответствующий собственный вектор действительной матрицы А.В методе скалярных произведенийвместе с матрицей А используется транспонированная матрица АТ.
Алгоритм метода скалярных произведений:
1) зададим начальные приближения: х0 – ксобственному вектору матрицы А и у0 = х0– к собственному вектору транспонированной матрицы АT;
k = 0;
2) вычислим (k + l)-e приближение к наибольшему собственному значению λпо формулам
xk +1= Ахk,yk +1 =ATyk, λk = 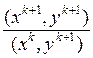 , k = k +1; (3.41)
, k = k +1; (3.41)
3) если |λk+1- λk| ³ ε, переходим к п. 2, иначе – к п. 4;
4) конец.
7.Вычисление всех собственных значений положительно определенной симметричной матрицы
Приведем алгоритм для вычисления нескольких первых или всех собственных значений и соответствующих собственных векторов положительно определенной симметричной матрицы.

 Пусть уже вычислены первые m собственных значений λ1, λ2, ..., λm и т соответствующих собственных векторов x1, x2, ..., xm.
Пусть уже вычислены первые m собственных значений λ1, λ2, ..., λm и т соответствующих собственных векторов x1, x2, ..., xm.
Алгоритм вычисления очередного (т + 1)-го собственного значения и
соответствующего собственного вектора:
0) выберем начальное приближение 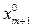 ; k = 0;
; k = 0;
1) вычислим k-e приближение к собственному значению λm+1:
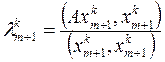 ; (3.42)
; (3.42)
2) находим вектор 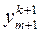 из уравнения
из уравнения
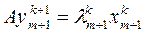 ; (3.43)
; (3.43)
3) если m > 0, ортогонализируем вектор 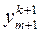 к первым т собственным векторам:
к первым т собственным векторам:
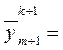
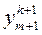 -
- 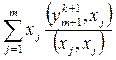 ; (3.44)
; (3.44)
4) нормируем полученный вектор:
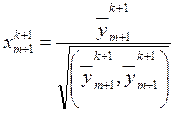 ; (3.45)
; (3.45)
5) k = k+1.
Процесс 1–5 повторяется до тех пор, пока не будет выполнено условие сходимости итераций
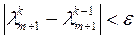 (3.46)
(3.46)
где ε – заданная погрешность.
При вычислении первого собственного значения и соответствующего вектора п. 3 пропускается.
Этим алгоритмом можно вычислить все собственные значения и собственные векторы.
| <== предыдущая лекция | | | следующая лекция ==> |
| Алгебраические и трансцендентные уравнения | | | Приближение функций |
Дата добавления: 2020-08-31; просмотров: 936;











