Сферические координаты.
Эта система очень сильно похожа на географические координаты на планете. Если соединим точку 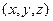 кратчайшей линией теперь не с осью
кратчайшей линией теперь не с осью 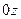 , а с точкой
, а с точкой 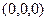 , и именно это расстояние обозначим
, и именно это расстояние обозначим 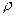 , то чертёж получается несколько иной, чем в прошлом случае.
, то чертёж получается несколько иной, чем в прошлом случае.
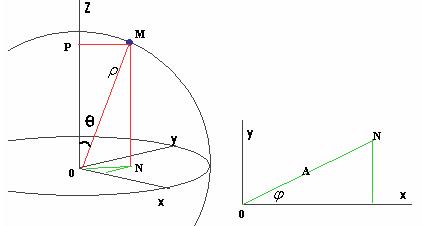
Угол между отрезком, соединяющим 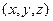 с началом координат, и вертикальной осью, обозначим
с началом координат, и вертикальной осью, обозначим 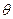 (греческая буква «тетта»), а угол в горизонтальной плоскости между осью
(греческая буква «тетта»), а угол в горизонтальной плоскости между осью 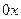 и его проекцией обозначим
и его проекцией обозначим 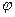 .
.
Координата 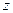 , равная расстоянию OP, это прилежащий катет угла
, равная расстоянию OP, это прилежащий катет угла 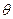 ,
, 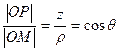 таким образом,
таким образом, 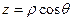 .
.
Расстояние PM = ON, обозначенное буквой А на правом чертеже, это противолежащий катет, поэтому 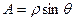 . А в треугольнике в плоскости
. А в треугольнике в плоскости 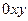 , это А является гипотенузой, где
, это А является гипотенузой, где 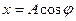 ,
, 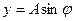 . Поэтому в итоге получаем:
. Поэтому в итоге получаем:
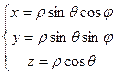 .
.
Здесь 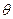 это и есть
это и есть 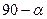 , если
, если 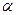 географическая широта. В этой системе «широта» фактически отмеряется от северного полюса, на экваторе она равна 90 градусов, а на южном полюсе 180. Угол
географическая широта. В этой системе «широта» фактически отмеряется от северного полюса, на экваторе она равна 90 градусов, а на южном полюсе 180. Угол 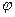 это аналог географической долготы.
это аналог географической долготы.
Диапазоны изменения таковы: 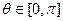 ,
, 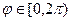 ,
, 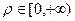
Рассматривать 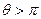 нет смысла, потому что до этой же самой точки можно будет от северного полюса провести более короткую дугу с другой стороны, по другому мередиану, при
нет смысла, потому что до этой же самой точки можно будет от северного полюса провести более короткую дугу с другой стороны, по другому мередиану, при 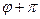 .
.
Для сферических координат якобиан: 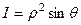 . Выведем в качестве задачи на практике.
. Выведем в качестве задачи на практике.
Известно, что площадь сферы пропорциональная квадрату расстояния от центра, и как видим, в определителе Якоби присутствует 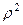 . Появление
. Появление 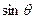 также не случайно и физически понятно: ведь при приближении к полюсу, площадь сегмента сферы между соседними широтами меньше, чем на экваторе. Так, между 0 и 10 градусов помещается много экваториальных стран, а длина экватора 40 тыс.км, а вот между 80 и 90 градусов - очень небольшая территория, и параллель 800 намного короче, чем 100.
также не случайно и физически понятно: ведь при приближении к полюсу, площадь сегмента сферы между соседними широтами меньше, чем на экваторе. Так, между 0 и 10 градусов помещается много экваториальных стран, а длина экватора 40 тыс.км, а вот между 80 и 90 градусов - очень небольшая территория, и параллель 800 намного короче, чем 100.
Пример. С помощью сферических координат вывести формулу объёма шара 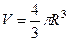 .
.
Решение. В этом примере надо рассматривать функцию 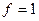 .
.
Для шара, 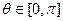 ,
, 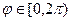 ,
, 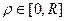 .
.
Функция равна 1, и её умножаем на якобиан.
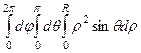 =
= 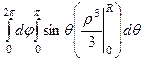 =
= 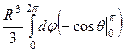 =
=
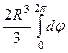 =
= 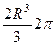 =
= 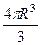 .
.
Дата добавления: 2017-04-05; просмотров: 2215;











