Приложения определённых интегралов.
Пункт 1. Вычисление площадей фигур.
Так как площадь криволинейной трапеции связана с интегралом, то это приложение очевидно. Но есть особенности, связанные со строением геометрической фигуры, в некоторых случаях надо разбить фигуру на несколько частей.
Пример. Найти площадь фигуры, ограниченной линиями 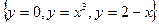 .
.
Решение. Построим чертёж:
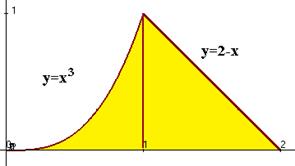
Так как верхняя граница после точки 1 переходит с одной кривой на другую, то придётся разбить на сумму двух вычислений по каждой части отдельно: 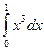 +
+ 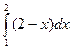 . Итак, получим
. Итак, получим 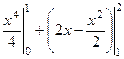 =
= 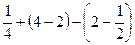 =
= 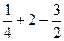 =
= 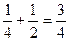 .
.
Пункт 2. Вычисление объёмов тел вращения.
Если график функции вращать вокруг оси 0x, то получится так называемое тело вращения. Каждое сечение плоскостью, паерпендикулярной оси 0x , это круг, его площадь равна 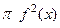 , так как
, так как 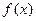 это как раз и есть радиус (равно удалению вращающейся точки от оси вращения). В итоге,
это как раз и есть радиус (равно удалению вращающейся точки от оси вращения). В итоге, 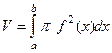 .
.
Пример. Вывести этим методом формулу объёма шара 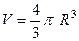 .
.
Решение. Чтобы получить шар, достаточно вращать верхнюю полуокружность, которая задаётся такой функцией: 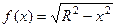 .
.
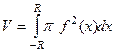 =
= 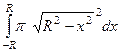 =
= 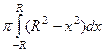 =
=
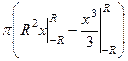 =
= 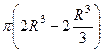 =
= 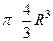 .
.
Пункт 3. Вычисление длины дуги кривой.
Формула для явно заданной кривой: 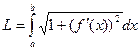 .
.
Доказательство.Разобьём область определения на n частей, рассмотрим подробнее одну часть графика.
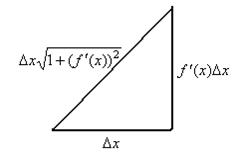
Длина фрагмента кривой приближённо равна гипотенузе. При этом, тангенс угла наклона равен производной. Поэтому, если горизонтальный катет 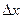 то вертикальный равен
то вертикальный равен 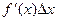 . Но в этом случае гипотенуза, по теореме Пифагора, равна:
. Но в этом случае гипотенуза, по теореме Пифагора, равна:
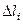 =
= 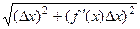 =
= 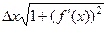 .
.
При переходе к пределу при 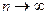 , получится
, получится 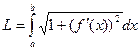 .
.
Чем круче наклон фрагмента графика, тем больше величина 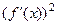 , и тем больше корень
, и тем больше корень 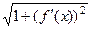 и соответственно, длина части этой кривой. Напротив, если график горизонтальный (функция = константа) то
и соответственно, длина части этой кривой. Напротив, если график горизонтальный (функция = константа) то 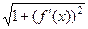 =
= 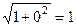 . Длина такой кривой просто равна длине отрезка в области определения, то есть
. Длина такой кривой просто равна длине отрезка в области определения, то есть 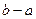 .
.
Для параметрически заданной в плоскости формула принимает такой вид: 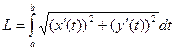 .
.
В трёхмерном пространстве: 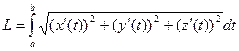 .
.
Длина кривой в полярной системе координат.
Пусть кривая задана формулой 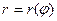 .
.
Тогда: 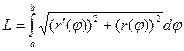 .
.
Доказательство этой формулы. Рассмотрим формулы взаимосвязи между полярными и декартовыми координатами:
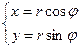
Теперь применим параметр 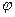 таким же образом, как в прошлой формуле был параметр
таким же образом, как в прошлой формуле был параметр 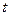 .
.
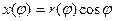 ,
, 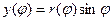 .
.
Найдём производные:
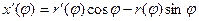
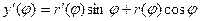
Их надо подставить в формулу: 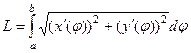 .
.
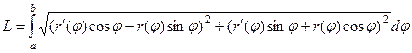
применим формулу сокращённого умножения в каждом квадрате под корнем. Там получатся квадраты и удвоенные произведения, которые, впрочем, сократятся, ведь они будут разного знака. Выражение под корнем преобразуется так:
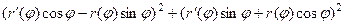 =
=
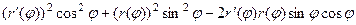 +
+
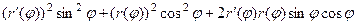 =
=
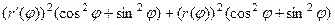 =
=
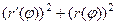 .
.
Поэтому и получается в итоге: 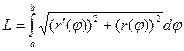 .
.
ЛЕКЦИЯ № 4. 07.03.2017
Дата добавления: 2017-04-05; просмотров: 1398;











