Декартовы координаты.

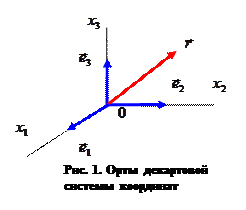Координатные поверхности декартовой системы координат в пространстве трёх измерений являются плоскими поверхностями, каждая из которых перпендикулярна остальным координатным поверхностям. Координатные линии (линии пересечения координатных поверхностей) представляют собой систему взаимно перпендикулярных прямых линий. Координатные линии размечены с использованием масштаба длины, масштаб длины выбирают одинаковым для всех координатных линий, разметка предполагается равномерной. Из начала координат (точка О) вдоль координатных линий проведём единичные безразмерные векторы - орты - 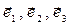. Предполагаем, что операции скалярного и векторного произведения определены безотносительно вида конкретной системы координат.

Для правой системы координат справедливы соотношения (символическая форма правил выполнения скалярного и векторного произведения двух векторных величин известна читателю):

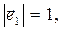
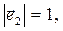
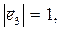
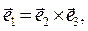
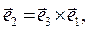
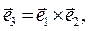(1)

,

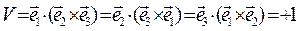где 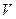- «объём» прямоугольного параллелепипеда, построенного на ортах декартовой системы координат. Следствием соотношений (1) является свойство ортогональности ортов декартовой системы координат:

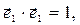
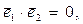
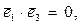
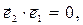
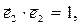
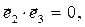(2)

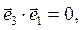
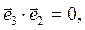
Соотношения (2) в компактной форме записи имеют вид:

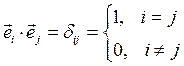(3)

Соотношения (2) или (3) действительно имеют место. Например, для случая i=2, j=1 имеем: 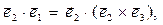но 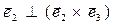по определению, поэтому скалярное произведение рассматриваемых ортов обращается в нуль.

Свойство ортогональности ортов декартовой системы координат позволяет осуществить разложение произвольного радиус-вектора на составляющие вдоль координатных направлений:

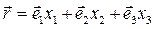. (4)

Разложение радиус-вектора (4) становится определённым, если указано правило определения коэффициентов разложения x₁, x₂ и x₃. В рамках «геометрического» подхода можно воспользоваться методом параллельного проектирования, который лежит в основе операций сложения и разложения векторных величин. В рамках «алгебраического» подхода рассмотрим скалярное произведение одного из ортов декартовой системы координат на радиус-вектор (4):

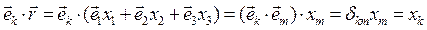. (5)

В выражениях (5) по повторяющемуся индексу m=1,2,3предполагается суммирование. Таким образом, получено соотношение

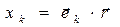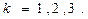, (6)

В соответствии с определением скалярного произведения векторов и определением понятия «орт» получаем

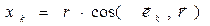. (7)

В формуле (7) 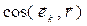является направляющим косинусом вектора 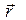относительно координатного направления, описываемого ортом .

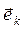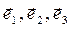Если в качестве ортов декартовой системы координат использованы единичные безразмерные векторы , то размерность коэффициента разложения 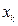радиус-вектора 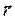совпадает с размерностью модуля радиус-вектора, а алгебраическая величина коэффициента разложения 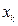представляет собой длину отрезка Оx_k, откладываемого в положительном или отрицательном направлении от начала координат вдоль рассматриваемого координатного направления.

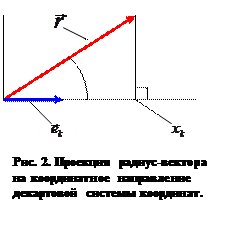
Особенностью декартовой системы координат является то обстоятельство, что коэффициент разложения 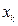, как это видно из рассмотрения рисунка 2, получается и с помощью «ортогонального» (перпендикулярного) проектирования радиус-вектора на соответствующее координатное направление, но при этом перпендикуляр к координатному направлению 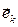оказывается параллельным плоскости, в которой лежат два остальных орта. В рассматриваемом случае «параллельное» проектирование и «ортогональное» проектирование приводят к одному и тому же результату, поэтому в декартовых системах координат нет нужды различать координаты радиус-вектора, полученные тем или иным способом проектирования вектора на выбранное координатное направление.