Поверхностные волны

Шторм всегда охватывает ограниченную часть поверхности океана. По мере усиления ветра в зоне его действия зарождаются и растут волны. Через некоторое время после того как ветер установился, волнение делается статистически стационарным. Это значит, что средняя высота волн, их средняя длина и средний период не изменяются. Однако мгновенные состояния водной поверхности в зоне действия ветра выглядят хаотическими. В отдельный момент времени эта поверхность представляет собой сложное беспорядочное чередование валов, впадин и холмов различной высоты и горизонтального простирания. При переходе к последующим моментам геометрия водной поверхности меняется случайным, непредсказуемым образом. В силу сказанного к изучению волн в зоне их генерации ветром применим только статистический подход. Методы теории вероятностей и многочисленные наблюдения позволили получить на этом пути ряд полезных результатов. Было установлено, что распределение вероятностей высот волн следует функции распределения Релея. Ее интегральным выражением служит формула

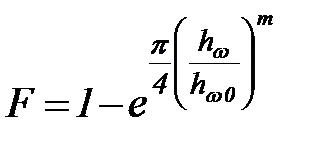(96)

где: h_w – высота волн с вероятностью непревышения F;

h_{w 0} – средняя высота волн.

Показатель степени m меняется от 4 на глубокой воде до 2 на мелкой. Средняя высота волн h_{w 0} может быть найдена по дополнительным соотношениям, основанным на балансе энергии волн. Согласно наблюдениям во время штормов высоты океанических волн нередко превышают 10 м. При ураганах отдельные волны могут достигать высоты 20-25 м.

Время Т, за которое волна продвигается на свою длину l, называется периодом волны. Средний период и средняя длина волн в зоне их генерации ветром выражаются соответственно эмпирическими формулами, связывающими эти величины со скоростью ветра:

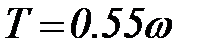(97)

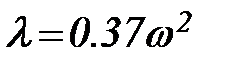(98)

Численные коэффициенты в этих формулах размерные, скорость ветра w имеет размерность м/с.

Чем длиннее волна, тем быстрее она движется в океане и тем медленнее рассеивается ее энергия. Поэтому наиболее крупные волны из возникающих в зоне шторма могут выходить за пределы этой зоны и удаляться на большие расстояния от места своего зарождения. Такие волны называются волнами зыби. Когда ветер прекращается, первыми затухают короткие волны и через некоторое время в районе закончившегося шторма остаются тоже только волны зыби. Волны зыби являются упорядоченными образованиями. Они имеют вид параллельных валов с формой, близкой к синусоидальной, и следуют друг за другом через приблизительно равные расстояния.

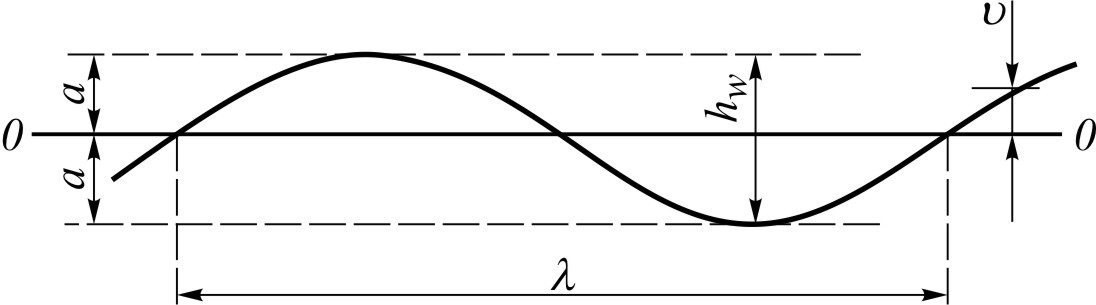Рис. 56. Профиль синусоидальной волны

Правильный характер волн зыби позволяет с достаточной точностью описать их свойства методами гидродинамики. Профиль синусоидальной волны и его элементы показаны на рис. 56. Буквой x обозначена высота свободной поверхности относительно уровня покоя. При распространении синусоидальных волн x меняется по пути х и во времени t согласно закону

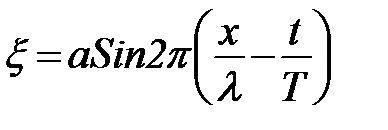, (99)

где: a – амплитуда (полувысота) волн.

Скорость распространения синусоидальных волн, в общем случае, выражается формулой

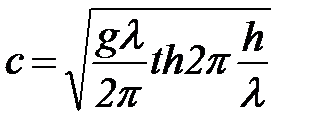. (100)

Если глубина водоема велика по сравнению с длиной волн, т.е. 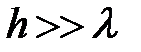, то 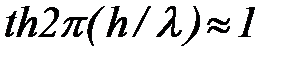, и формула (100) переходит в следующую:

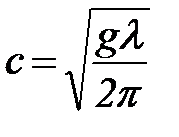. (101)

Если, наоборот, 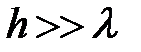, то 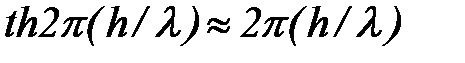, и вместо формулы (100) мы имеем

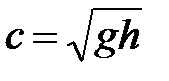. (102)

Таким образом, в глубоких водоемах скорость распространения волн определяется их длиной, а в мелких – глубиной водоема. За условную границу между глубокими и мелкими водоемами принимается глубина, равная половине длины волны: 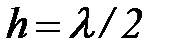. Над океаническим ложем океан всегда глубок для ветровых волн, но он становится «мелким», когда в нем распространяются волны цунами.

Так как длины волн зыби могут составлять от нескольких десятков до нескольких сот метров, то согласно формуле (101) скорости их перемещения обычно лежат в интервале 10-20 м/с. Это значит, что за сутки волны зыби могут пройти более 1500 км.

При подходе к берегу волны трансформируются. Их гребни заостряются, ложбины становятся плоскими. При глубине воды, равной 1,5-2,0 высотам волн, волны разбиваются.

Если волны в открытом океане или море, а также в открытой части озера или водохранилища распространяются вдоль берега, то на береговой отмели они разворачиваются.

Гребни волн стремятся стать параллельными береговой линии, скорость волн получает составляющую, направленную к берегу (рис. 57). Это

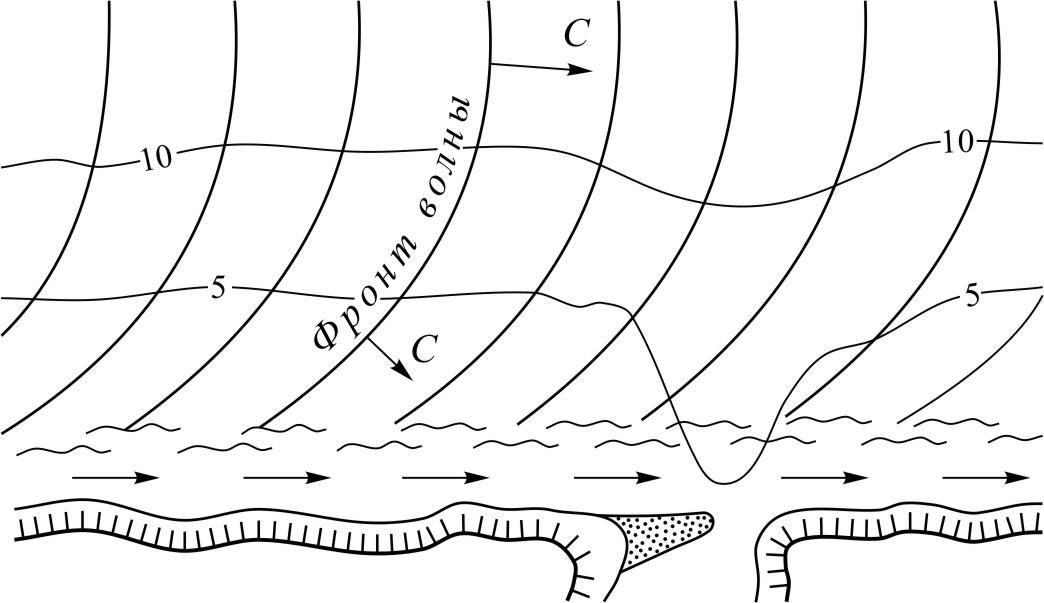Рис. 57. Рефракция волн на береговой отмели

явление носит название рефракции волн на береговой отмели. Объяснение рефракции волн дает формула (102). Скорость волны над склоном дна оказывается переменной вдоль гребня – ближайшие к берегу участки гребня движутся медленнее, удаленные от берега – быстрее.

Подходя к берегу под острым углом и разбиваясь, волны создают вдольбереговое течение воды (см. рис. 57). Скорости вдольберегового потока могут достигать 1,0-1,5 м/с. Эти скорости достаточны для интенсивного транспорта наносов, и вдольбереговые течения перемещают на морских побережьях, а также в береговых зонах озер и водохранилищ большие массы грунта. Когда вдольбереговой поток встречает устье залива или бухты, он откладывает здесь свой груз или часть его и входы в заливы и бухты после штормов мелеют.

Приливы и отливы

Два раза в сутки Мировой океан обегает приливная волна. Период приливной волны равен половине лунных суток: 12 ч 25 мин, или 44700 с. Большая длина лунных суток по сравнению с солнечными объясняется тем, что Луна вращается по своей орбите в том же направлении, в котором вращается Земля. По большому кругу земного шара, лежащему в плоскости орбиты Луны, приливная волна движется со средней скоростью 450 м/с. Эту скорость нельзя получить по формуле (102), так как приливы и отливы представляют собой вынужденные колебания, а не свободные, как волны зыби или сейши.

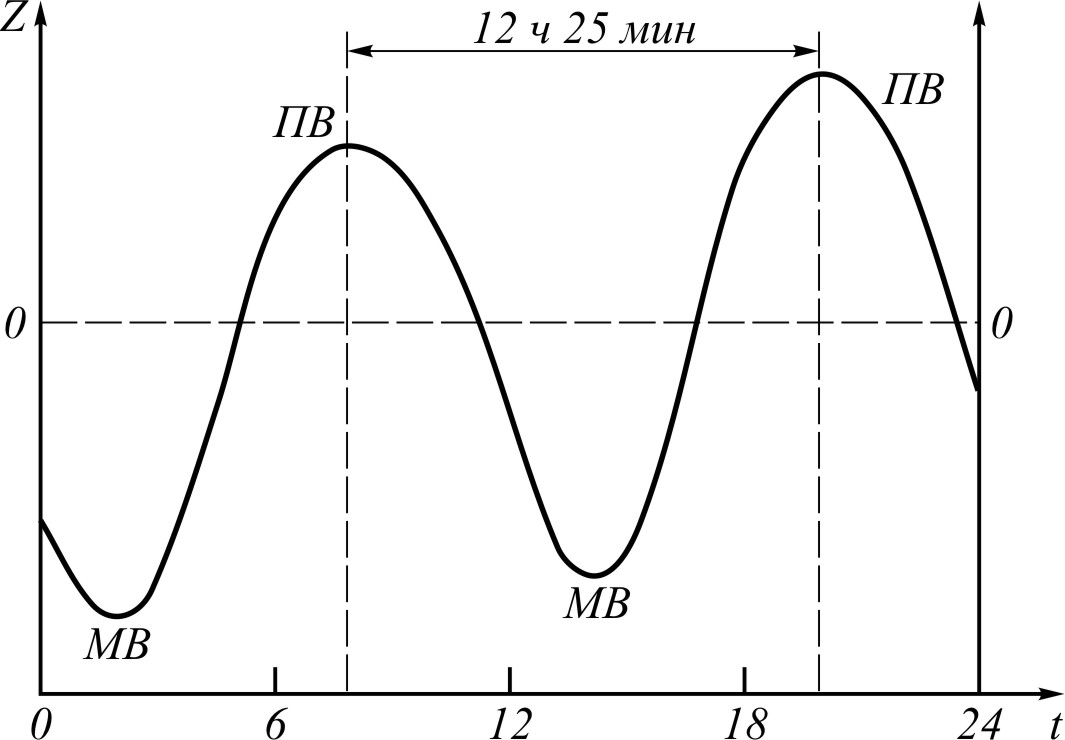Рис. 58. Ливные колебания уровня океана

Обычно наблюдающийся ход ливных колебаний уровня воды показан на рис. 58. Наивысший уровень при приливе называют полной водой ПВ, наинизщий при отливе – малой водой MB. Колебания уровней несколько запаздывают по отношению к движению Луны. Время между кульминацией Луны и полной водой называется лунным промежутком. Он меняется в течение месяца и года, а также по акватории океана. Когда склонение Луны равно нулю (плоскость орбиты Луны совпадает с плоскостью экватора), высота двух полусуточных полных вод одинакова. При ненулевом склонении (а оно меняется от 0° до ±28°) высоты двух полных вод различны.

Приливные волны порождаются двумя небесными телами – Солнцем и Луной и распространяются по сферической поверхности. Одни эти обстоятельства, не говоря уже о неравномерном распределении глубин океана и неправильности его границ, придают ливным колебаниям чрезвычайно сложный характер. К проявлениям этой сложности относится тот факт, что наряду с показанными на рис. 58 полусуточными колебаниями, в океане при определенных условиях образуются суточные колебания – с одной полной и одной малой водой в сутки.

Разность между высотой полной и малой воды называется величиной прилива. В открытом океане величина прилива невелика. У небольших океанических островов она редко превышает 1 м. Наибольших значений величина прилива достигает у берегов океанов и морей, особенно в бухтах, заливах и узкостях. На протяжении морских границ СССР наибольшая величина прилива – до 12 м – наблюдается в Пенженской губе Охотского моря. Величины 8-10 м достигают приливы в устье Мезени. В устьях больших сибирских рек Оби, Енисея и Лены ливные колебания уровней значительно слабее сгонно-нагонных колебаний.

В Западной Европе наиболее высокие приливы создаются на Атлантическом побережье Франции и у берегов Англии. Величина прилива в Бристольском заливе доходит до 15 м. Самые высокие приливы на земном шаре – до 18 м – наблюдаются в бухте Фанди на Атлантическом побережье Канады.

Рассмотрим механизм ливных колебаний уровня океана. Силы, вызывающие эти колебания, называются приливообразующими. Они обусловлены притяжением Луны и Солнца, но как сейчас будет показано, отнюдь не равны самим силам притяжения. Кроме них, в образовании ливных колебаний участвуют центробежная и кориолисова силы инерции и силы трения. Приливообразующая сила, создаваемая притяжением Луны, вследствие близости Луны к Земле в 2,3 раза больше приливообразующей силы, создаваемой Солнцем. Абсолютные значения приливообразующих сил очень малы. При отнесении к единице массы они измеряются стомиллионными долями ускорения свободного падения на Земле.

Чтобы уяснить существо явления, разберем действие на воду в океане притягивающего тела и в качестве такого возьмем Солнце, так как законы движения планет вокруг Солнца позволяют очень просто решить вопрос о центробежных силах, обусловленных этим движением (если бы мы взяли за притягивающее тело Луну, то обнаружили бы, что Земля и Луна вращаются вокруг общего центра масс, находящегося внутри Земли, и определение центробежных сил стало бы очень сложным).

Примем, не внося погрешности в существо наших рассуждений, что плоскость экватора совпадает с плоскостью орбиты Земли, и выделим в этой плоскости диаметр Земли, направленный в данный момент времени

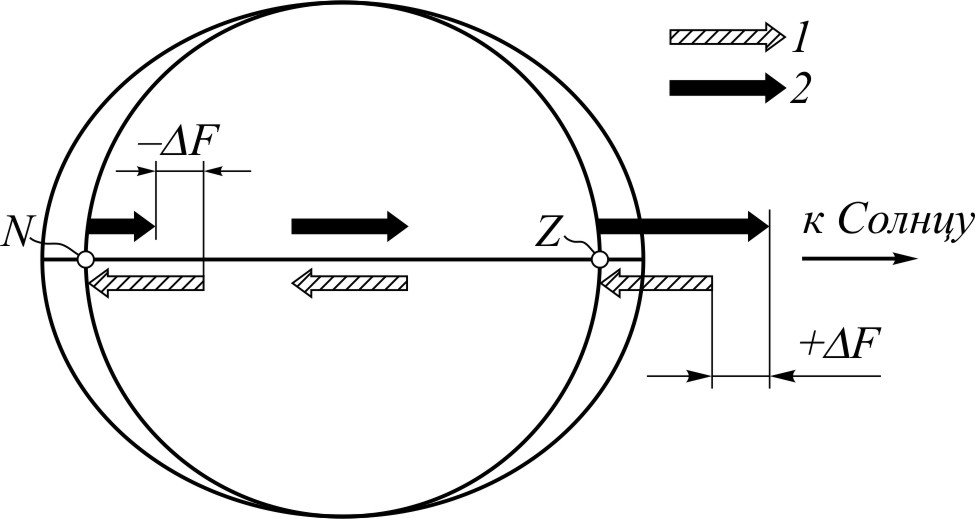Рис. 59. К происхождению приливообразующих сил: 1 – сила притяжения; 2 – центробежная сила

на Солнце (рис. 59). Вдоль выделенного диаметра действуют центробежная сила и сила притяжения Солнца. Вследствие законов обращения планет все точки Земли имеют одинаковые орбитальные траектории и поэтому центробежная сила, вызываемая орбитальным движением во всех точках земного шара, и значит во всех точках нашего диаметра, одна и та же. 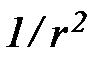Что касается силы притяжения, то от конца диаметра, обращенного к Солнцу, – точки зенита Z – к его другому концу – точке надира N она должна убывать как , где r – расстояние точки от центра Солнца. Основываясь на малости диаметра Земли (»13 тыс. км) по сравнению с расстоянием от Земли до Солнца (149 млн. км), допустимо пренебречь нелинейностью этого изменения и принять, что сила притяжения в зените будет больше, а в надире меньше силы притяжения в центре Земли на одну и ту же величину DF. В центре Земли сила притяжения и центробежная уравновешены, на земной поверхности равновесия, очевидно, не получается. В зените, где сила притяжения больше центробежной, их результирующая DF направлена к Солнцу, в надире – DF направлена от Солнца. Силы ±DF и есть приливообразующие. Общее определение приливообразующих сил следующее: приливообразующей силой в данной точке земного шара называется векторная разность между силой притяжения небесного светила (Солнца или Луны) в данной точке и силой его притяжения в центре Земли. В конечном счете, за образование приливов ответственна неоднородность поля тяготения.

Описанное распределение приливообразующих сил приводит к тому, что в каждый момент времени свободная поверхность Мирового океана имеет два диаметрально противоположных горба. Эти горбы в системе отсчета, связанной с Солнцем, в течение суток почти не меняют своего положения, а в системе отсчета, связанной с вращающейся Землей, они движутся против направления вращения, создавая эффект двух полусуточных волн прилива.

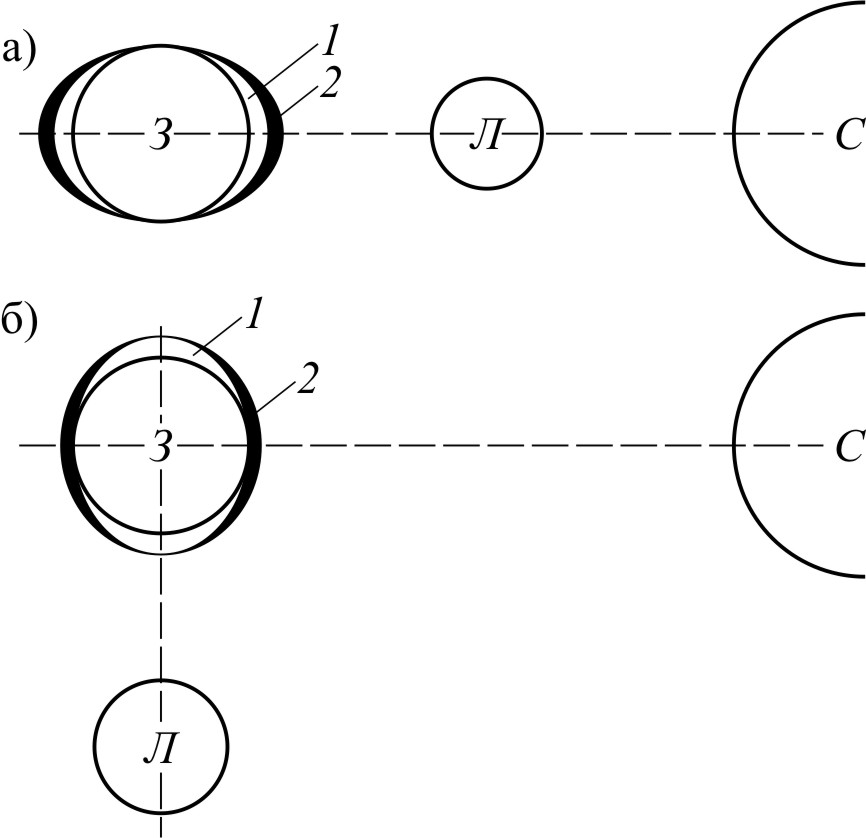Рис. 60. К объяснению месячного неравенства приливов: а – астрономическая сизигия; б – астрономическая квадратура; 1 – приливная волна, создаваемая Луной; 2 – приливная волна, создаваемая Солнцем

Качественно таково же влияние на воды океана и притяжения Луны. Так как взаимное расположение трех светил – Солнца, Земли и Луны – периодически изменяется, то периодически изменяется также сумма двух приливообразующих сил, а с ней и величина приливов. Наиболее существенно так называемое месячное неравенство приливов. Оно состоит в следующем. В новолуние и полнолуние три тела – Солнце С (рис. 60), Земля 3 и Луна Л – расположены на одной прямой. Это состояние называется астрономической сизигией. Приливообразующие силы Луны и Солнца во время сизигии складываются, и через 1-2 дня после нее приливы достигают наибольшей величины. Они называются сизигийными. В первую и последнюю, четверть Луны направление Земля – Луна образует прямой угол с направлением Земля – Солнце. Такая конфигурация трех тел называется астрономической квадратурой. При квадратуре две приливообразующие силы не складываются: оси двух пар горбов перпендикулярны и вскоре приливы снижаются до минимальных величин. Такие приливы называются квадратурными.

Сказанное в этом параграфе может дать лишь общее представление о приливах. Теорией приливов занимались многие выдающиеся механики и математики (И. Ньютон, Д. Бернулли, П. Лаплас, Г. Эри, Г. Пуанкаре и др.), однако нельзя считать эту теорию завершенной. Выполненные теоретические работы и многочисленные наблюдения позволили составить карты приливов и справочники, которые широко используются в мореплавании. Карты и справочники продолжают пополняться и уточняться.

Отметим одну из интересных и еще недостаточно изученных сторон теории приливов – проблему сил трения, развивающихся при движении приливных волн. По имеющимся оценкам мощность, теряемая на трение в приливных волнах Мирового океана, составляет немалую цифру: 1,1×10⁶ МВт. Трение между Землей и приливными волнами тормозит вращение Земли и считается причиной того увеличения длительности суток на 0,001 с за столетие, которое установлено астрономическими наблюдениями.