Установившийся приток реального газа к горизонтальной скважине по линейному и нелинейному законам фильтрации

В соответствии с аналогией фильтрации несжимаемой жидкости и реального газа [66] известные решения для фильтрации несжимаемой жидкости легко преобразуются для фильтрации газа. Для этого необходимо объемный расход заменить весовым 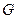, а отношение 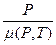- обобщенной функцией Лейбензона:

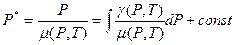. (1.1)

С учетом уравнения газового состояния:

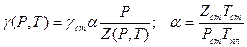(1.2)

функция (1.1) принимает следующий вид:

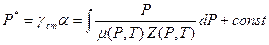, (1.3)

где 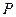-давление;

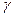- удельный вес газа;

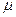- коэффициент абсолютной вязкости;

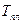- пластовая температура газа;

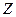- коэффициент сверхсжимаемости газа;

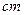- символ, означающий стандартные условия.

Интеграл (1.3) рассчитывается численным способом. Усредняя параметры 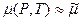и 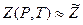и применяя их к функции (1.3) для преобразования, например, формулы притока нефти к горизонталь­ной скважине, получаем формулу дебита горизонтальной газовой скважи­ны:

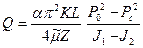. (1.4)

Установившийся приток реального газа к горизонтальной скважине по нелинейному закону фильтрации.Задача решается по двухзонной схеме притока к горизонтальной скважине, дренирующей полосообразный однородно-анизотропный пласт с двухсторонним симметричным контуром питания (рис. 1.1). Получено следующее уравнение притока:

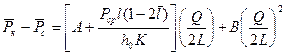, (1.5)

где

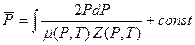, (1.6)

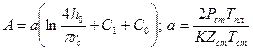; (1.7)

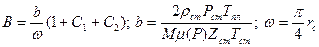; (1.8)

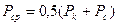. (1.9)

Усредняя параметры 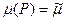и 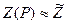, интегрируя (1.6) в пределах от 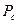до 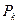, получаем выражение для левой части уравнения при­тока (1.5):

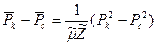. (1.10)

Здесь 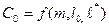- добавочные фильтрационные сопротивления, обуслов­ленные перфорацией колонны [26], (рис. 1.1);

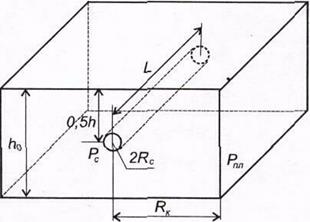
Рис. 1.1. Модель горизонтальной скважины

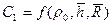- добавочные фильтрационные сопротивления, обуслов­ленные относительным расположением горизонтального ствола [26];

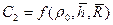- добавочные фильтрационные сопротивления, обуслов­ленные нелинейным законом фильтрации [26].

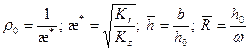, (1.11)

где

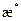- коэффициент анизотропии пласта;

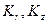-коэффициенты проницаемости по горизонтали и вертикали

соответственно;

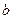-расстояние от кровли пласта до положения горизонтального ство­ла;

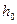- горизонтальная толщина продуктивного пласта.

Установившийся приток реального газа с учетом содержания кислых компонентов.Наличие кислых компонентов оказывает существенное влияниена точность определения обобщенной функции Лейбензона:

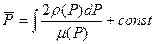, (1.12)

где плотность газа 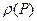определяется по формуле (1.2).

Решая совместно (1.2) и (1.12), посленекоторых преобразований получаем выражение:

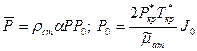, (1.13)

где

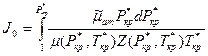, (1.14)

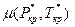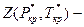и коэффициенты абсолютной вязкости и сверхсжимаемости как функции приведенных псевдокритических давлений 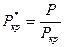и температур ;

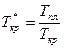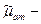усредненный коэффициент абсолютной вязкости газа в поверхностных условиях.

С учетом (1.13) и (1.14) левая часть уравнения притока (1.5) при­нимает следующий вид:

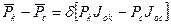, (1.15)

где

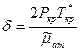, (1.16)

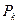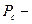и пластовое и забойное давление соответственно;

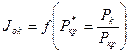и 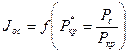определяются по формуле (1.14).

1.2. Приближенное аналитическое решение Алиева-Шеремета задачи притока реального газа к горизонтальной скважине по нелинейному закону фильтрации

Двухзонная схема притока. Рассматривается работа горизон­тальной скважины, эксплуатирующей полосообразный пласт, схематично показанной на рис. 1.2. В точной постановке решение такой задачи сопряжено с большими трудностями. Поэтому использованы некоторые упрощающие предположения, практически не искажающие физический смысл процесса фильтрации газа при нелинейном законе к горизонтальной скважине. Для этого истинная область фильтрации газа заменена такой фиктивной областью, в которой суммарное сопротивление пласта эквивалентно истинному фильтрационному сопротивлению [2].

При этом схема притока газа к горизонтальной скважине делится на две зоны: в первой зоне (рис. 1.2а) на расстоянии 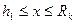, где 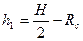- фильтрация газа принимается плоскопараллельной; во второй зоне 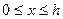естественная толщина пласта заменяется фиктивной пе­ременной толщиной, а скважина-галереей высотой 2 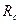[2]. Принятый характер изменения 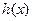во второй области описывается формулой:

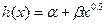, (1.17)

где 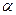и 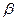- постоянные коэффициенты, определяемые из граничных усло­вий.

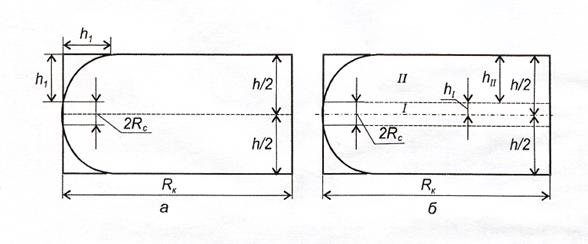
Рис. 1.2. Схема притока газа к горизонтальной скважине

(по Алиеву и Шеремету)

Для случая, когда ствол скважины симметрично расположен по от­ношению к кровле и подошве пласта, эти коэффициенты могут быть опре­делены для четверти показанной схемы задачи, исходя из условий:

при ; при ;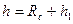

тогда коэффициенты равны: 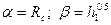и, следовательно,

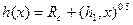. (1.18)

Для принятой схемы в первой зоне зависимость между градиентом давления и скоростью фильтрации будет иметь вид:

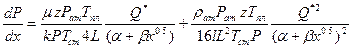, (1.19)

где 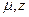-коэффициенты вязкости и сверхсжимаемости газа;

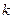- коэффициент проницаемости;

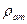-плотность газа при стандартных условиях;

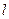- коэффициент макрошероховатости;

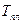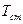, - соответственно пластовая и стандартная температура.

Интегрируя в пределах от 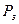до 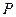(давления на границе I и II зоны) и

от 0 до 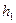, получаем:

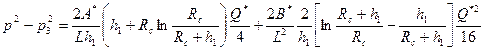, (1.20)

где

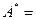
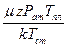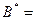
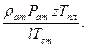; (1.21)

Для второй зоны, где происходит плоскопараллельное движение газа, связь между давлением и дебитом представлена в виде следующего выра­жения:

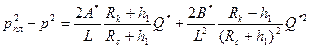. (1.22)

Из уравнений (1.20) и (1.22) получаем связь между давлением и де­битом 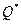для всей зоны:

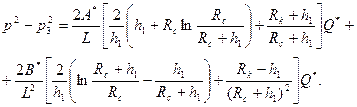(1.23)

Учитывая, что 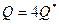, получаем расчетную формулу:

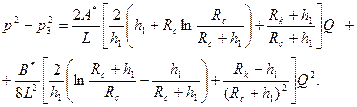(1.24)

Введем обозначения:

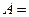
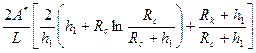; (1.25)

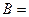
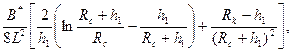
где .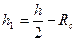

С учетом (1.25) вместо (1.24) получаем формулу для определения дебита горизонтальной скважины, вскрывшей изотропный пласт и симмет­рично расположенной по отношению к его кровле и подошве:

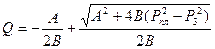. (1.26)

Формула (1.26) не учитывает сопротивления ствола скважины при движении потока газа по стволу. При больших длинах горизонтальной час­ти ствола и дебитах газа потери давления в стволе скважины могут оказать очень сильное влияние на ее дебит.

Влияние анизотропии на производительность скважины [42, 37, 38] . Теперь рассмотрим влияние анизотропии пласта на производительность горизонтальных газовых скважин. Принимаем, что коэффициент анизотропии:

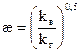(1.27)

пропорционально изменяет газонасыщенную толщину пласта. Тогда преды­дущая задача, решенная для изотропного пласта с учетом анизотропии, бу­дет иметь следующий вид:

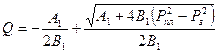, (1.28)

где

;

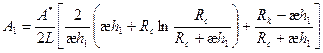(1.29)

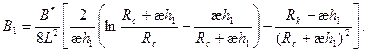
Анализ формулы (1.29) показывает, что с уменьшением параметра анизотропии дебит скважины существенно снижается, а при стремлении 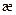к нулю коэффициенты 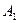и 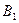принимают вид:

. (1.30)

Определение забойного давления в горизонтальной газовой и газоконденсатной скважинах. Точность определения забойного давления, как в вертикальных, так и в горизонтальных скважинах зависит от структуры потока газожидкостной смеси, режима потока, фазового состоя­ния смеси и других факторов. Кроме того, на точность определения забой­ного давления горизонтальных скважин существенно влияет степень радиу­са кривизны, и оснащенность горизонтальной части ствола фонтанными трубами, другими словами, конструкция скважины.

В работе [67] рассмотрены следующие схемы определения забойного давления горизонтальных скважин (давления у торца горизонтального ствола):

— скважина с большим радиусом кривизны и без фонтанных труб с горизонтальной части;

— скважина с большим радиусом кривизны и частично оборудован­ная фонтанными трубами в горизонтальной части;

— скважина со средним радиусом кривизны;

— скважина с малым радиусом кривизны.

1.3. Методика расчета оптимальной длины горизонтального участка ствола скважины в зависимости от расхода закачивае­мого газа в ПХГ [39]

В последнее время значительное число месторождений осваивается с использованием горизонтальных скважин. Техническая возможность буре­ния горизонтальных скважин позволила изменить стратегию освоения газо­вых месторождений, в том числе и подземных газовых хранилищ. При этом актуальной задачей остается обоснование длины горизонтально ствола скважин в зависимости от геолого-физических условий объекта эксплуата­ции, а также режимов работы скважин.

Аналитическое решение задачи. Для расчета оптимальной длины горизонтального участка ствола скважины принимаются и обосно­вываются все необходимые геометрические исходные данные.

Определяется длина дуги кривизны от точки вертикального ствола до точки перехода в горизонтальный ствол по формуле:

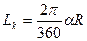, (1.31)

где 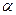- угол между вертикальным стволом и касательной в точке перехода к кривизне.

Рассчитываются показател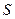и 2 и 2 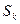в уравнении Адамова [68] по формулам:

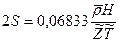, (1.32)

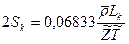. (1.33)

Формулы Адамова для давлений на забое по вертикальному стволу в точке перехода к горизонтальному 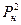и 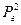записываются соответственно:

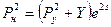; (1.34)

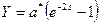; (1.35)

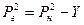; (1.36)

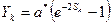; (1.37)

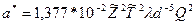. (1.38)

В формулах (1.32)-(1.38) принимаются следующие размерности:

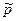- относительная плотность газа;

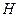- глубина вертикального ствола,м;

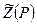- средняя величина сверхсжимаемости газа;

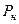- давление на забое вертикального ствола, кгс/см²;

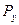- давление на устье нагнетательной скважины, кгс/см²;

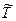- средняя температура по стволу работающей скважины, °К;

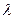- коэффициент гидравлического сопротивления в вертикальных трубах;

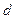- внутренний диаметр фонтанных труб (эксплуатационной колон­ны), см;

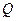- расход закачиваемого газа, тыс. м³ /сут;

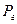-давление в пласте в точке перехода к горизонтальному стволу, кгс/см².

Параметры 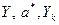имеют размерности (кгс/см²)². Решая совместно (1.34)-(1.38), переходя к размерности МПа, полу­чаем выражение для пластового давления в начале горизонтального ствола:

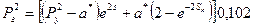. (1.39)

Для горизонтального ствола в работе [2] получено решение для схе­мы прямоугольного пласта (рис. 1.3):

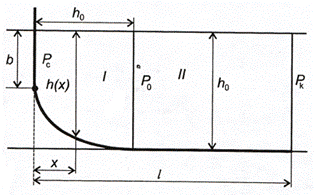
Рис. 1.3. Схема притока к несовершенной галерее и горизонтальной скважине

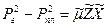, (1.40)

где

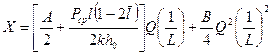. (1.41)

Обозначая правую часть уравнения (1.39) через

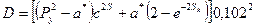(1.42)

и решая совместно (1.39) и (1.40), исключаем величину 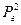, вконечномсчете, получаем квадратное уравнение относительно :

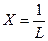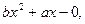(1.43)

где

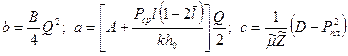; (1.44)

здесь 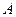и 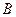- фильтрационные сопротивления для горизонтального ствола, которые имеют вид:

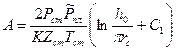; (1.45)

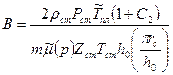; (1.46)

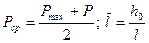, (1.47)

где 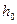- толщина газонасыщенного пласта;

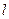- расстояние от горизонтального ствола до контура питания с двусторонним притоком в прямоугольном полосообразном пласте;

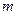- коэффициент микрошероховатости пласта:

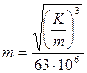, (1.48)

где 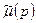- коэффициент абсолютной вязкости газа;

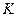- проницаемость пласта;

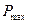- предельно-допустимое давление в пласте;

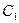- добавочное фильтрационное сопротивление, обусловленное относительным положением горизонтального ствола;

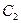- добавочное фильтрационное сопротивление, обусловленное

нарушением линейного закона Дарси.

Положительный корень квадратного уравнения (1.43) представляется в виде:

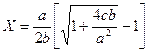(1.49)

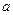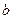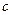или, вводя соответствующие обозначения и учитывая значения , и по

формулам (1.44), получаем после ряда преобразований:

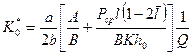; (1.50)

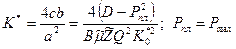. (1.51)

С учетом (1.50) и (1.51) зависимость протяженности 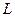горизон­тального ствола от расхода 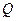, согласно (1.49), записывается в виде:

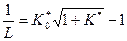. (1.52)