Графические способы изображения статистических данных

При полевых наблюдениях и во время камеральной обработки фактического материала в распоряжение геоморфологов поступают количественные данные по морфометрии рельефа, условиям залегания горных пород, по вещественному и гранулометрическому составу рыхлых толщ и пр. Необходимо осуществлять массовый сбор таких данных, чтобы их можно было подвергнуть статистической обработке, позволяющей значительно обогатить результаты проведенных геоморфологических исследований.

Первичные статистические материалы сводят в таблицы, в которых отмечают распределение совокупности полученных данных по определенным группам в зависимости от принятых показателей. На основании таблиц составляют различного рода графики (диаграммы, кривые), которые дают наглядное представление о результатах проведенного статистического изучения.

Кривые распределения. При обработке статистических данных выделяют совокупности однородных (т, е. обладающих качественной общностью) величин или элементов. Сюда относятся, например, совокупности величин, характеризующих форму и размеры зерен в обломочных породах, форму и размеры неровностей земной поверхности. Каждую такую совокупность делят на ряд групп пли классов со свойственными им значениями признака, или вариантами.

Варианты характеризуются определенной частотой, т. е. абсолютной численностью группы (класса) или его относительной численностью (по отношению к сумме численности всех групп или классов). Распределение признака внутри данной совокупности называют вариационным рядом. Таким образом, вариационный ряд показывает частоту, т. с. абсолютное или относительное количество элементов совокупности при определенных значениях признака, или вариантах.

Вариация признака может быть прерывистой (дискретной) и непрерывной. Вариация дискретна, если значения признака у двух элементов совокупности совпадают либо отличаются друг от друга не менее чем на определенную величину. Вариация непрерывна, если значение признака у двух элементов совокупности отличаются друг от друга на любую малую величину (например, величина зерен в обломочных породах).

Непрерывную вариацию можно представить в виде ряда частот, из которых каждая относится не к определенному точному значению признака, а к интервалу его изменения. В таком случае говорят о групповых, или классовых, вариантах.

В вариационном ряду каждому значению признака (или каждому интервалу) соответствует определенная частота. Эту связь можно изобразить графически в прямоугольной системе координат. По горизонтальной оси откладывают значения признака, а по вертикальной — его частоты. Горизонтальная ось графика с нанесенными на пен делениями называется шкалой. Шкалы бывают равномерные, сели равным числовым интервалам соответствуют равные отрезки шкалы, и неравномерные, когда равным числовым интервалам соответствуют неодинаковые отрезки шкалы.

Очень часто употребляют логарифмическую неравномерную шкалу, у которой расстояния от ее начала до точек пропорциональны не самим числам, а их логарифмам. Такая шкала удобна, когда графически изображают данные, резко отличающиеся по абсолютной величине.

Так, при построении графика гранулометрического состава с укрупнением зерен приходится сильно увеличивать интервалы (разности конечных размеров) выделяемых фракций. Для их изображении берут логарифмическую шкалу, и в этом случае график называется полу логарифмическим. Если же логарифмы величин откладываются и по горизонтальной, и по вертикальной оси, то график называют логарифмическим.

Графики распределения частот по отдельным интервалам изменения признака называются графиками дифференциального распределения или гистограммами. Они имеют вид столбиков, у которых основание соответствует интервалу изменения признака, а высота — его частоте. Через вершины столбиков можно провести плавную кривую дифференциального распределения (рис. 4, А).

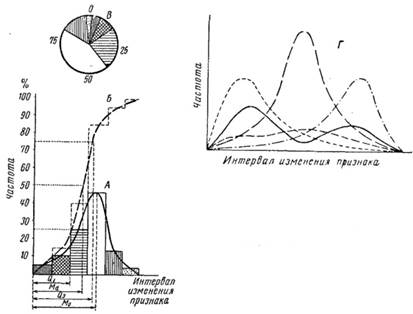
Рис. 4. Различные виды графических изображений. А — гистограмма; Б — кумулятивная кривая; В — циклограмма; Q₁ и Q₃ — первая и третья квартили; M_d — медиана; М_о — мода; Г — различные виды кривых распределения

Если по вертикали откладывать не отдельные частоты, а их сумму от ее минимального значения до величины при каждом последующем интервале, получится восходящая ступенчатая линия или плавная кривая, которую называют графиком интегрального распределения или кумулятивной кривой (рис. 4,Б).

Форма кривой распределения позволяет судить о характере изучаемой совокупности. Дифференциальные кривые бывают: плавные без резко выраженной вершины; с одной четко очерченной вершиной, расположенной симметрично или Же смещенной к началу или к концу графика; с двумя вершинами (рис. 4, Г). Одновершинные кривые свидетельствуют об однородности распределения, тогда как наличие у кривой двух и более вершин говорит о том, что они охватывают не одну, а две и более разнородных совокупностей.

Однородную совокупность характеризуют следующие показатели:
1. Средняя арифметическая (Мα). Для определения средней арифметической каких-либо величин х₁ х₂, ..., х_n, входящих в данную совокупность, сумму этих величин делят на их число n:

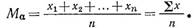
Если каждый член совокупности встречается в ней несколько раз, то определяют взвешенную среднюю арифметическую. Для этого служит формула

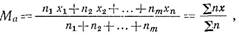
где хи х₁ х₂, ..., х_n — члены данной совокупности, n₁, n₂,… n_m — частота их нахождения.

В практике геолого-геоморфологических исследований приходится определять взвешенную среднюю арифметическую окатанности галек и других количественных показателей форм рельефа и отложений.

2. Мода (М_О). Модой данной совокупности называют значение признака с наибольшей частотой, т. е. наиболее часто встречающееся значение признака. На кривой дифференциального распределения эта величина равна абсциссе, соответствующей наибольшей ординате данной кривой (см. рис. 4).

3. Медиана (M_d). Медианой называют значение признака, который делит данную совокупность на две равные части. Графически эту величину находят по кумулятивной кривой, проведя горизонтальную линию через деление ординаты, равной 50%. Абсцисса точки пересечения этой линии с кумулятивной кривой и есть медиана (см. рис. 4).

4. Среднее отклонение. Этот показатель характеризует степень однообразия данной совокупности. Аналогичное значение имеет коэффициент сортировки, который часто определяют по формуле

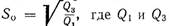
— соответственно первая и третья квартили, значение которых находят по кумулятивной кривой.

Для этого па графике через деления 25% и 75% на ординате проводят параллельные линии. Абсциссы их пересечения с кривой и есть искомые величины первой и третьей квартилей. Коэффициент сортировки для положительных величин всегда больше единицы, и чем он сильнее отклоняется от единицы, тем менее однообразна (менее сортирована) соответствующая совокупность.

Для характеристики состава сложных совокупностей, состоящих из качественно разнородных компонентов (например, петрографического или минерального состава обломочных отложений), применяют столбиковые и круговые диаграммы (рис. 4, Б).

Для изображения результатов статистического изучения условий залегания горных пород, пространственной ориентировки форм и элементов рельефа используют полярные диаграммы и диаграммы - розы.

Полярные диаграммы позволяют показать азимут и угол падения пластов, косых слойков и склонов. Они имеют вид круга, внутри которого проведены концентрические окружности, соответствующие углам падения названных объектов. Круг пересекают радиусы, указывающие азимут падения от 0 до 360°. Каждый замер изображается в виде точки по двум ее координатам— углу и азимуту падения. По группировке точек судят о закономерностях ориентировки и величине падения изучаемых объектов (см. рис. 42).

Диаграммы-розы показывают частоту ориентировки изучаемого объекта, например трещин, тальвегов эрозионных форм и пр. Их строят следующим образом. Проводят концентрические окружности, отвечающие частотам ориентировки объектов в процентах, и серию радиусов-векторов, причем направление последних соответствует среднему азимуту выбранного интервала.

Так, при интервале 15° проводят радиусы-векторы через 7,5°, 22,5°, 37,5° и т. д.; при интервале 10°—соответственно 5°, 15°, 25° и т. д. На каждом радиусе-векторе точкой отмечают количество замеров азимута внутри данного интервала в процентах. Точки соединяют линиями и, таким образом, получают диаграмму-розу, на которой наглядно выявляется преобладающая ориентировка изучаемых объектов (см. рис. 41).

При геолого-геоморфологических исследованиях применяют и другие графические способы изображения результатов исследований. Некоторые из них рассматриваются в последующих главах этой книги.