Политропный процесс

Расчет процессов базируется на первом и втором началах термодинамики, записанных в дифференциальной форме для одного килограмма термодинамической системы:

,

.

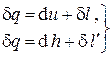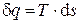Входящие в эти выражения дифференциалы вычисляются следующим образом:

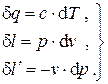
Кроме того, для идеального газа имеем

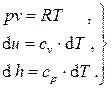
На практике чаще всего имеют дело с термодинамическими процессами, в течение которых на каждых малых участках процесса можно с достаточной точностью считать постоянным соотношение между количествами работы и теплоты. Такие процессы называют политропными. Для них

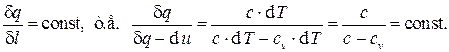
Поскольку для идеального газа 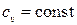, уравнение политропного процесса может быть записано в виде

,

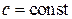т.е. политропный процесс можно определить как процесс с постоянной теплоемкостью, которая может принимать любые значения, .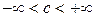

Соотношения между параметрами в политропном процессе можно получить на основании уравнений политропного процесса в переменных 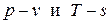. Используем для этого две формы записи I начала термодинамики:

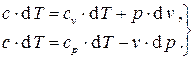
Перенеся слагаемые с 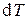в левые части этих выражений и разделив второе уравнение на первое, получим

.

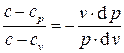Комплекс (постоянный в случае политропного процесса)

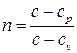
носит название показателя политропы. Имеем, таким образом

.

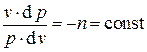Разделяя переменные в этом уравнении и интегрируя, получаем связь между давлением и объемом в политропном процессе:

.

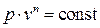Получим уравнение политропного процесса в переменных 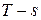из уравнения для второго закона термодинамики:

,

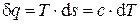Откуда .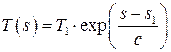

Обычно на практике политропный процесс задается не значением теплоемкости c, а значением показателя политропы n, тогда теплоемкость процесса вычисляется как

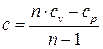или ,

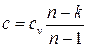где величина 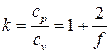определена ранее.