Лекция №3. ПОЛОЖЕНИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Случайная величина, которая в зависимости от случая принимает те или иные значения с определенной вероятностью. Случайные величины могут иметь различный характер. Случайная величина может быть, например:
· скалярной величиной;
· вектором;
· функцией;
· и др.
С каждой случайной величиной можно связать определенное событие.
Событие, которое может произойти или не произойти в результате данного опыта, называется случайным. Количественной оценкой возможности появления случайного события 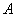 служит вероятность
служит вероятность 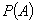 .
.
Вероятностью события 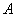 называют отношение числа случаев
называют отношение числа случаев 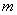 , благоприятствующих этому событию, к числу n всех возможных случаев в данном опыте:
, благоприятствующих этому событию, к числу n всех возможных случаев в данном опыте:
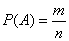 .
.
При этом все случаи должны быть равно возможны, несовместимы и независимы.
Вероятность события является объективной мерой его возможности и определяется в предположении проведения очень большого числа опытов, в результате которых появляется данное событие, поэтому эта величина имеет теоретический характер.
Практической характеристикой возможности случайного события 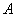 служит частость события
служит частость события 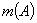 , представляющая собой отношение частоты
, представляющая собой отношение частоты 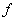 появления события
появления события 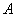 к общему числу
к общему числу 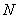 проведенных опытов:
проведенных опытов:
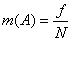 .
.
Между вероятностью и частотой какого-либо события существует приближенное равенство:
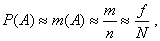
которое будет тем точнее, чем больше число опытов.
Характеристикой случайной величины служит закон ее распределения.
Под распределением случайной величины понимают совокупность ее значений, расположенных в возрастающем порядке, с указанием либо их вероятностей в теоретическом, либо частостей в практическом распределении.
Практическое распределение случайных величин дискретного характера можно представить в виде таблицы или графика.
Таблица Практическое распределение дискретной случайной величины
| X | ||||||
| m(xi) | 1/20 | 3/20 | 8/20 | 5/20 | 3/20 | 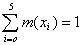
|
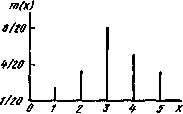
Рисунок Распределение случайной дискретной величины
Распределение случайной величины непрерывного типа может быть также представлено в виде таблицы или графика. Для составления таблицы практического распределения непрерывной случайной величины в совокупности ее значений находят max и min и определяют разность между ними. Разность эта называется полем рассеивания 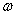 случайной величины:
случайной величины:
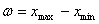 .
.
Значения случайной величины, составляющие совокупность, делят на равные интервалы. Их число « 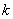 » определяют из отношения значения
» определяют из отношения значения 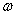 к избранному значению «
к избранному значению « 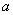 » интервала:
» интервала:
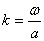 .
.
Относя каждое значение случайной величины к тому или иному интервалу, подсчитывают частоты ее значений в границах интервалов и определяют частости значений 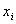 . Например. Пусть в партии валов из 100 штук диаметр одной из шеек
. Например. Пусть в партии валов из 100 штук диаметр одной из шеек 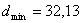 мм, а другой
мм, а другой 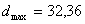 мм. Тогда
мм. Тогда 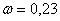 мм.
мм.
При избранном значении интервала 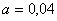 мм число
мм число 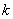 будет равно:
будет равно:
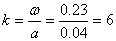 .
.
Установив границы и подсчитав частости, получают таблицу распределения значений 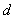 вала:
вала:
| 1) | 32,13 – 32,16 | 0,03 | |
| 2) | 32,17 – 32,20 | 0,11 | |
| 3) | 32,21 – 32,24 | 0,36 | |
| 4) | 32,25 – 32,28 | 0,40 | |
| 5) | 32,29 – 32,32 | 0,6 | |
| 6) | 32,33 – 32,36 | 0,04 |
Графически практическое распределение непрерывной случайной величины может быть представлено либо гистограммой, либо практической кривой (полигоном) распределения.
Общей формой закона распределения случайной величины является ее функция распределения. Функцией распределения или интегральным законом распределения скалярной случайной величины 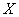 называют вероятность выполнения неравенства
называют вероятность выполнения неравенства 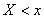 :
:
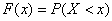 ,
,
где 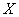 – случайная величина,
– случайная величина,
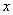 – возможные значения случайной величины.
– возможные значения случайной величины.
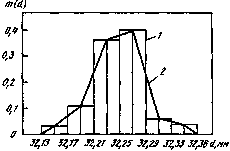
Рисунок Гистограмма и практическая кривая распределения непрерывной случайной величины
Для дискретной случайной величины 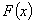 может быть найдено по таблице или графику распределения для любого значения
может быть найдено по таблице или графику распределения для любого значения 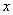 , как сумма вероятностей тех значений
, как сумма вероятностей тех значений 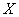 , которые лежат влево от точки с координатой
, которые лежат влево от точки с координатой 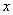 . В рассмотренном выше примере распределения случайной величины для
. В рассмотренном выше примере распределения случайной величины для 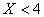 .
.
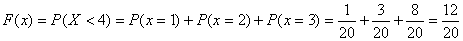 .
.
Интегральный закон распределения можно представить в виде графика 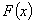 . Для дискретной случайной величины график будет иметь вид ступенчатой кривой.
. Для дискретной случайной величины график будет иметь вид ступенчатой кривой.
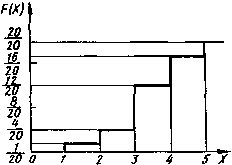
Рисунок Интегральный закон распределения дискретной случайной величины
Имея функцию распределения дискретной случайной величины можно вычислить вероятность ее нахождения в границах от 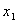 до
до 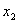 :
:
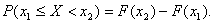
Для непрерывной случайной величины график функции распределения будет иметь вид монотонно возрастающей кривой, а сама функция будет дифференцируемой.
Производную 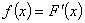 функции распределения
функции распределения 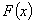 непрерывной случайной величины
непрерывной случайной величины 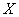 называют плотностью вероятности или дифференциальным законом распределения этой случайной величины.
называют плотностью вероятности или дифференциальным законом распределения этой случайной величины.
Графически этот закон распределения может быть представлен кривой линией, построенной в координатах x, 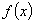 .
.
Зная плотность вероятности, можно определить вероятность того, что значение случайной величины 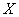 окажется в интервале от
окажется в интервале от 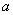 до
до 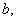 .
.
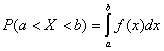 .
.
В данном случае вероятность равна площади участка с основанием « 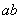 », ограниченного сверху кривой плотности вероятности. При
», ограниченного сверху кривой плотности вероятности. При 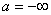 и
и 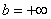 :
:
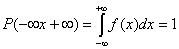 .
.
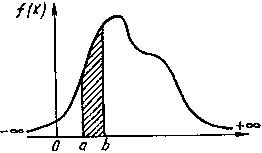
Рисунок Дифференциальный закон распределения непрерывной случайной величины
Дифференциальный закон или плотность вероятности дает полную картину распределения случайной величины. Однако такая полная характеристика не всегда необходима. В ряде теоретических и практических задач бывает достаточным знание отдельных числовых характеристик:
определяющих положение центра группирования случайной величины 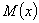 ;
;
ее рассеяние около этого центра.
Для характеристики положения центра группирования используют математическое ожидание и среднее арифметическое значение случайной величины:
а) для дискретной случайной величины:
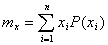 ,
,
где 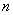 – число возможных значений случайной величины
– число возможных значений случайной величины 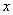 ;
;
б) для непрерывной случайной величины:
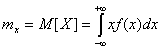 ,
,
где 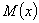 – характеристика теоретического распределения случайной величины.
– характеристика теоретического распределения случайной величины.
На практике положение центра группирования 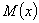 характеризует среднее арифметическое значение случайной величины:
характеризует среднее арифметическое значение случайной величины:

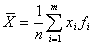 ,
,
где 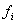 – частота отдельных значений
– частота отдельных значений 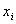 ,
,
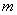 – число отдельных значений
– число отдельных значений 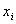 ,
,
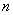 – общее отдельных значений
– общее отдельных значений 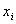 .
.
Характеристикой рассеяния значений случайной величины около центра группирования 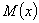 является дисперсия. Однако чаще используют не саму дисперсию, а положительный квадратный корень из нее, называемый средним квадратичным отклонением:
является дисперсия. Однако чаще используют не саму дисперсию, а положительный квадратный корень из нее, называемый средним квадратичным отклонением:
а) дисперсия и среднее квадратичное отклонение дискретной случайной величины
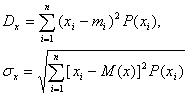 ;
;
б) дисперсия и среднее квадратичное отклонение непрерывной случайной величины
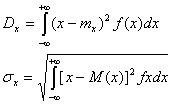 .
.
Для практических распределений среднее квадратическое отклонение определяется по формуле:
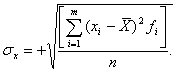
Размерность 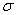 x совпадает с размерностью самой случайной величины.
x совпадает с размерностью самой случайной величины.
Таким образом, чтобы охарактеризовать распределение случайной величины надо иметь как минимум две числовые характеристики:
1. 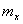 или
или 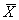 – определяют положение центра группирования;
– определяют положение центра группирования;
2. 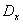 или
или 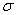 x – разброс значений случайной величины около центра группирования.
x – разброс значений случайной величины около центра группирования.
Комплектом характеристик распределения следует считать также:
поле рассеяния случайной величины:
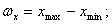
— координату середины поля рассеяния:
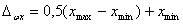 .
.
В симметричных распределениях центр группирования 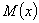 оказывается совмещенным с
оказывается совмещенным с 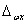 .
.
Распределение случайных величин в зависимости от условий могут подчиняться вполне определенным законам: Гаусса, равной вероятности, Симпсона. Наибольшее практическое значение в технологии машиностроения имеет дифференциальная функция закона нормального распределения (закон Гаусса), для которого плотность вероятности или дифференциальная функция распределения:
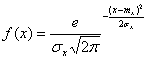 ,
,
где 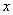 – переменная случайная величина;
– переменная случайная величина;
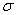 x – среднее квадратичное отклонение
x – среднее квадратичное отклонение 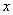 от
от 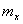 ;
;
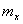 – математическое ожидание величины
– математическое ожидание величины 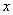 .
.
Дифференциальная функция закона нормального распределения графически изображается холмообразной кривой, симметричной относительно центра группирования, представленной величинами 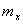 и
и 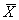 . Координата центра группирования определяет положение кривой относительно начала отсчета, а параметр
. Координата центра группирования определяет положение кривой относительно начала отсчета, а параметр 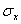 (среднее квадратичное отклонение) – ее форму и размах.
(среднее квадратичное отклонение) – ее форму и размах.
Функция или интегральный закон нормального распределения в общем виде можно записать:
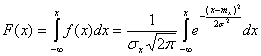 .
.
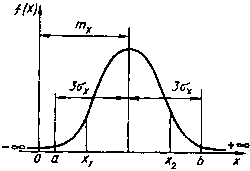
Рисунок Дифференциальный закон нормального распределения случайной величины
Закон равной вероятности встречается, когда наряду со случайными факторами, вызывающими рассеяние, действует доминирующий систематический фактор непрерывно или равномерно изменяющий во времени положение центра группирования 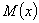 . Графически такое распределение случайной величины отображается прямоугольником.
. Графически такое распределение случайной величины отображается прямоугольником.
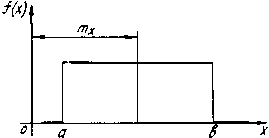
Рисунок Распределение случайной величины по закону равной вероятности
Математическое ожидание, дисперсия и среднее квадратичное отклонение соответственно равны:

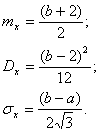
К распределению по закону Симпсона (закон треугольника) приводит сложение двух случайных величин, подчиненных закону равной вероятности при одинаковых параметрах рассеяния. Графически кривая рассеяния имеет вид равностороннего треугольника.
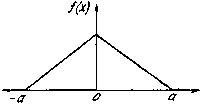
Рисунок Распределение случайной величины по закону Симпсона
Математическое ожидание, дисперсия и среднее квадратичное отклонение соответственно равны:
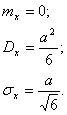
Если рассматривать распределение по законам Симпсона и равной вероятности как отклонение от закона нормального распределения, то можно отразить и количественную сторону этих отклонений с помощью коэффициента 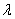 , который называется относительным средним квадратичным отклонением:
, который называется относительным средним квадратичным отклонением:
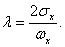
На практике чаще пользуются значением коэффициента возведенного в квадрат.
Таблица Значения относительного среднего квадратичного отклонения
| Закон распределения | 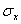
| 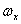
| 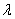
| 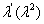
|
| Нормальный (Гаусса) | 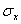
| 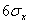
| 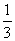
| 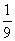
|
| Симпсона | 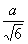
| 2a | 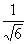
| 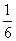
|
| Равной вероятности | 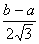
| b-a | 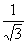
| 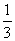
|
Дата добавления: 2017-04-05; просмотров: 2086;











