Лекция №10. РАССЧЕТ РАЗМЕРНЫХ ЦЕПЕЙ
Размерной цепью называется совокупность размеров, непосредственно участвующих в решении поставленной задачи и образующей замкнутый контур (ГОСТ 16319-80).
По виду задач, в решении которых цепи участвуют, они делятся на конструкторские, технологические и измерительные.
Конструкторские размерные цепи решают задачу по обеспечению точности при конструировании. Они устанавливают связь размеров детали в изделии.
Технологические размерные цепи решают задачу по обеспечению точности при
изготовлении машин. Они устанавливают связь размеров деталей на разных этапах
технологического процесса.
Измерительные размерные цепи решают задачу обеспечения точности при измерении. Они устанавливают связь между звеньями, которые влияют на точность измерения.
Замыкающее звено ( А∆, Б∆, В∆ и т.д.) – то звено, которое непосредственно не выдерживается, а получается в результате выполнения размеров составляющих звеньев. Размерная цепь всегда замкнута. На основании этого свойства существует зависимость, которая связывает номинальные размеры звеньев. Для плоских размерных цепей с номинальными звеньями она имеет следующий вид:
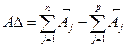
где n и p - число соответственно увеличивающих и уменьшающих звеньев в размерной цепи.
Для определения зависимости, которая связывает допуски звеньев в размерной цепи, найдем вначале наибольшее значение замыкающего звена:
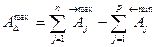
Наименьшее значение допуска: 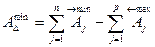
Вычтем AΔmin из AΔmax 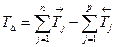
Верхнее отклонение: 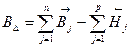
Нижнее отклонение: 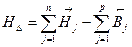
Координата середины поля допуска: 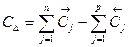
Допуск замыкающего звена: 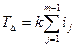
Значение k характеризует точность, с какой следует получать все составляющие звенья размерной цепи. Рассчитанное по формуле значение k в общем случае не будет соответствовать строго определенному квалитету, поэтому для назначения допусков на соответствующие звенья выбирают ближайшие квалитеты по табл. 4.1.
Метод полной взаимозаменяемости
Метод, при котором требуется точность замыкающего звена размерной цепи, получается при любом сочетании размеров составляющих звеньев. При этом предполагают, что в размерной цепи одновременно могут оказаться все звенья с предельными значениями, причем в любом из двух наиболее неблагоприятных сочетаний (все увеличивающие звенья с верхними предельными размерами, а уменьшающие с нижними, или наоборот). Такой метод расчета, который учитывает эти неблагоприятные сочетания, называется методом расчета на максимум - минимум.
Обратная задача.
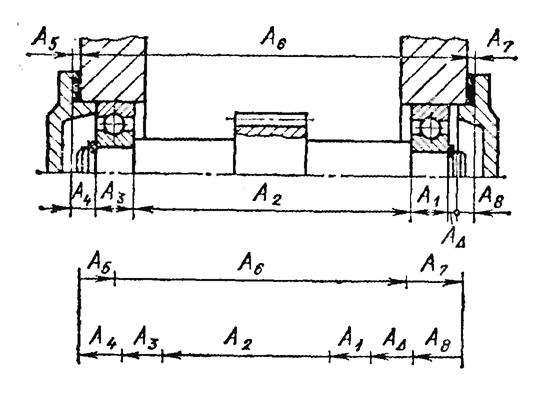
Расчет размерной цепи по методу полной взаимозаменяемости..
А1=А3=19-0,12, А2=150-0,08-0,24, А4=А8=10-0,06, А5=А7=1-0,015, А6=206+0,35+0,05
Номинальное значение AD:
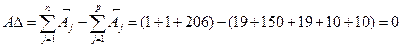
Допуск замыкающего звена:
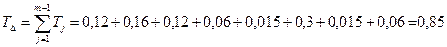
Координаты середины поля допуска:
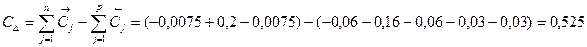
Верхнее отклонение:
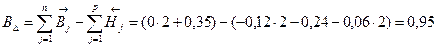
Нижнее отклонение:
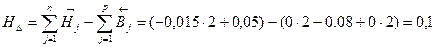
Проверка правильности решения:
Наибольшее значение замыкающего звена:
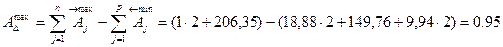
Наименьшее значение допуска:
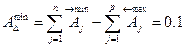
Прямая задача.
1. Определение номинальных размеров составляющих звеньев.
Номинальные размеры стандартных деталей, например, подшипников качения, находят по соответствующим стандартам. Остальные размеры составляющих звеньев, кроме звена А9→, определяют непосредственно по чертежу узла.
Для нахождения номинального размера А9→ воспользуемся зависимостью:
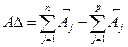
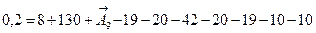
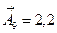
2. Определение средней точности размерной цепи.
По формуле найдем значение k :
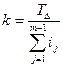
k=19,9
Найденное число единиц допуска лежит в пределах стандартных значений k =16 (7-й квалитет) и k = 25 (8-й квалитет). Отсюда следует, что часть звеньев должна изготавливаться по 7-му квалитету, часть – по 8-му. При этом следует назначать допуски таким образом, чтобы допуск звена A9→ лежал в пределах между 7-м и 8-м квалитетами либо соответствовал одному из этих квалитетов.
Предельные отклонения на составляющие звенья, кроме A9→, рекомендуется назначать на размеры, относящиеся к валам – по h, относящиеся к отверстиям – по H; на остальные ±IT/2, т.е. симметричные предельные отклонения.
Результаты поэтапных расчетов внесены в табл.
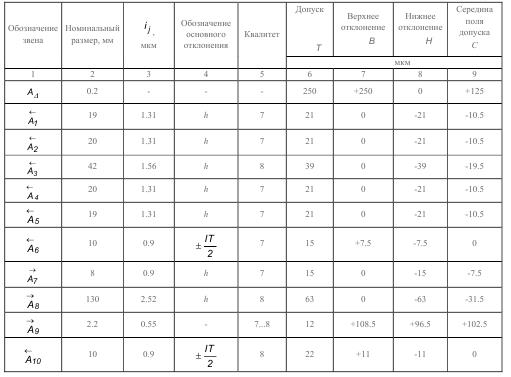
3. Определение допуска звена A9→ .
Воспользуемся формулой:
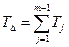
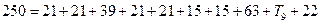
T9=12мкм.
4.Определение предельных отклонений звена А9→.
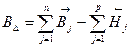
В9=+108,5
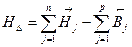
Н9=+96,5мкм.
5. Проверка. Чтобы убедиться в правильности проведенных расчетов, воспользуемся зависимостью для координат середины полей допусков :
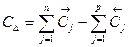
+125=+125
Метод неполной взаимозаменяемости
Это метод, при котором требуемая точность замыкающего звена размерной цепи получается не при любых сочетаниях, а при ранее обусловленной части сочетаний размеров составляющих звеньев.
Сборка осуществляется без пригонки, регулировки и подбора звеньев.
Метод исходит из предположения, что сочетание действительных размеров составляющих звеньев в изделии носит случайный характер, и вероятность того, что все звенья с самыми неблагоприятными сочетаниями окажутся в одном изделии, весьма мала.
Такой метод расчета, который учитывает рассеяние размеров и вероятность их различных сочетаний, называется вероятностным методом расчета. Другими словами, метод допускает малый процент изделий, у которых замыкающее звено выйдет за рамки поля допусков. При этом расширяются допуски составляющих цепь размеров, и тем самым снижается себестоимость изготовления деталей.
Задачей расчета является назначение допусков на составляющие звенья, соответствующих одинаковой степени точности.
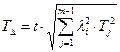
Формула устанавливает связь между допуском на замыкающий размер и допусками на составляющие звенья.
Для того чтобы добиться одинаковой точности составляющих звеньев размерной цепи, воспользуемся известной формулой Tj = k j ⋅i j и подставим ее в выражение. Потребуем, чтобы k у всех звеньев были одинаковыми, тогда :
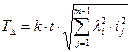
Окончательно:
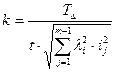
Значение k характеризует точность, с которой следует изготовить все составляющие звенья размерной цепи при заданных условиях.
При обработке деталей разброс размеров у них может распределяться и не по закону Гаусса. В этом случае можно также воспользоваться формулой, только при этом следует поставить другие значения 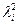 .
.
Если предполагается, что рассеяние размеров близко, например, к закону Симпсона, то 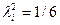 .
.
При неизвестном характере рассеяния размеров рекомендуется принимать закон равной вероятности с 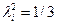 .
.
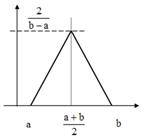
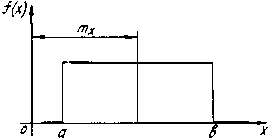
Распределение Симпсона. Распределение равной вероятности.
В зависимости от принятого процента риска P, значения t выбирают из ряда, приведенного в табл.

P – процент риска; t – коэффициент риска.
Пример
Вероятностный метод расчета рассмотрим на том же узле. По техническим
требованиям необходимо обеспечить осевой зазор ∆=+ A0 ,20,25. Требуется назначить допуски и отклонения на составляющие звенья при P = 0.27% и нормальном законе распределения рассеяния размеров составляющих звеньев (процент брака и закон распределения студент выбирает сам).
Решение
1. Определение номинальных размеров составляющих звеньев.
Этот пункт решения задачи полностью соответствует первому пункту при расчете на максимум - минимум.
2. Определение средней точности размерной цепи.
Воспользуемся зависимостью:
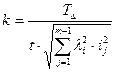
k=58,3
Найденное число единиц допуска k лежит ближе к стандартному значению k = 64 , что соответствует 10-му квалитету. Допуски на все звенья назначаются по 10-му квалитету.
3. Определение истинного процента брака.
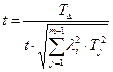
t=2,7
что соответствует 0.693% брака. Полагаем, что такой процент брака нас устраивает. Если же количество брака мы сочли бы чрезмерным, тогда необходимо было допуски на ряд звеньев назначить по 9-му квалитету. Результаты поэтапных расчетов внесены в табл.
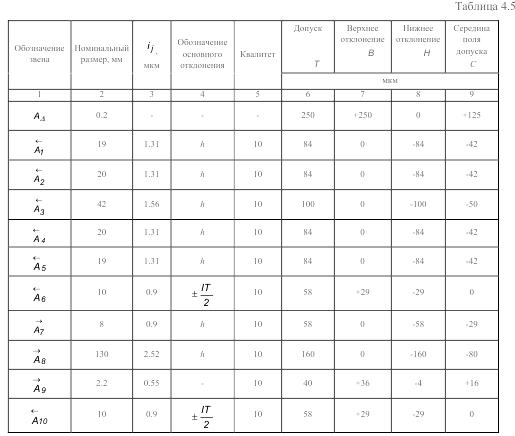
4. Определение предельных отклонений звена A9→.
Вначале определим координату середины поля допуска звена A9→ по формуле:
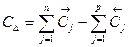
C9=+16
Верхнее отклонение:
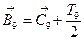 В9=36
В9=36
Нижнее отклонение:
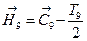 Н9=-4
Н9=-4
Метод пригонки
Это метод, при котором требуемая точность замыкающего звена размерной цепи достигается изменением размера компенсирующего звена путем снятия с компенсатора слоя металла. Его суть состоит в том, что допуски на составляющие звенья назначаются по экономически приемлемым квалитетам, например, по 12-14-му квалитетам. Получающийся после этого у замыкающего звена избыток поля рассеяния при сборке устраняют за счет компенсатора. Смысл расчета заключается в определении припуска на пригонку, достаточного для компенсации величины превышения предельных значений замыкающего звена и вместе с тем наименьшего для
сокращения объема пригоночных работ.
Роль компенсатора обычно выполняет деталь, наиболее доступная при разборке механизма, несложная по конструкции и неточная, например, прокладки, шайбы, проставочные кольца и т.п.
ПРИМЕР
Определить размеры заготовки компенсатора А9 для размерной цепи. Замыкающее звено должно быть А∆=0,2+0,25
Решение
1. Определение номинальных размеров составляющих звеньев.
Этот пункт решения задачи полностью соответствует первому пункту при расчете на максимум - минимум.
2. Выбор и назначение допусков на составляющие звенья.
Считаем, что для размеров звеньев экономически приемлемым является 12-й квалитет. Назначаем по этому квалитету допуски на все размеры, кроме допусков на монтажную высоту шариковых радиальных подшипников, и на звено A9→, которое выбрали в качестве компенсатора.
3. Определение наибольшей величины компенсации.
По формуле:
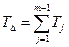
Нетрудно заметить, что сумма допусков составляющих звеньев значительно превосходит допуск Т∆ , т.е. колебание размера замыкающего звена от изделия к изделию значительно увеличится.
Наибольшая расчетная компенсация избыточного колебания размера замыкающего звена :
Т9’=-1510
Следовательно, при самом неблагоприятном сочетании размеров надо с компенсатора снять слой материала толщиной 1.51 мм, чтобы замыкающее звено попало в предписанные пределы.
Результаты расчетов представлены в табл.
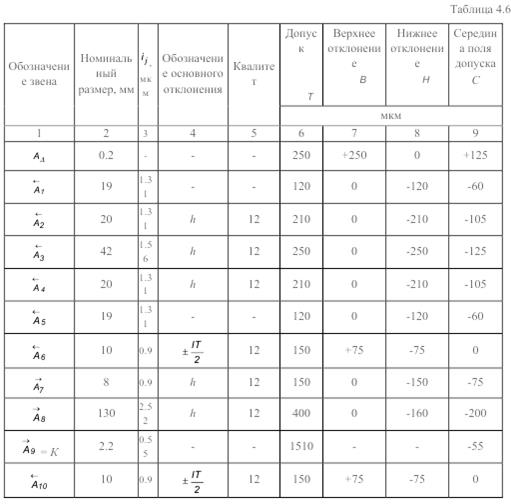
4. Определение предельных размеров компенсатора звена A9→.
Вначале определим координату середины поля допуска звена A9→:
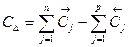
С9=-55
Минимальный размер компенсатора:
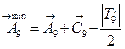 ,
, 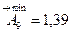
Максимальный размер:
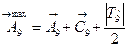 ,
, 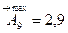
5. Определение размера заготовки компенсатора.
Исполнительный размер заготовки компенсатора определяется его наибольшей величиной, так как в прочих случаях он будет подгоняться.
Для изготовления компенсатора на него надо назначить приемлемый допуск, например, по тому же 12-му квалитету (IT12 = 0.1 мм), но так, чтобы его наименьший размер был не менее 2.9 мм :
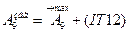 ;
; 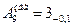
Метод регулирования с применением неподвижного компенсатора
Это метод, при котором требуемая точность замыкающего звена размерной цепи достигается изменением компенсирующего звена без снятия слоя металла.
Его суть состоит в том, что избыток поля рассеивания замыкающего звена устраняют путем подбора компенсатора из некоторого количества компенсаторов, заранее изготовленных с различными размерами.
Смысл расчета заключается в определении наименьшего количества компенсаторов в комплекте.
Пример
Определить размеры компенсационных прокладок в комплекте для размерной цепи. Замыкающее звено должно быть А∆=0,2+0,25
Решение
Прежним порядком (cм. метод пригонки) устанавливаем номинальные размеры и назначаем допуски на составляющие звенья размерной цепи. Рассчитываем величину компенсации Т9’=-1,51мм. и наименьший размер компенсатора в комплекте 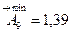 .
.
- Определение числа ступеней компенсации.
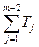 - сумма допусков всех составляющих звеньев без допуска на компенсатор; Тк – допуск на отдельный компенсатор в комплекте.
- сумма допусков всех составляющих звеньев без допуска на компенсатор; Тк – допуск на отдельный компенсатор в комплекте.
Допуск на отдельный компенсатор выбирается в пределах : Tk = (0,1…0,3)⋅T∆; мкм.
Тк=0,15.250=37,5мкм. Принимаем Тк=40 (10-й квалитет).
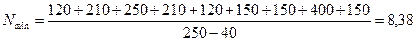
Число ступеней компенсации следует всегда округлять в большую сторону, так как по формуле (4.10) определяется наименьшее число ступеней. Принимаем: N=9.
2. Величина ступени компенсации.
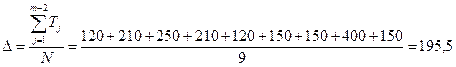 мкм.
мкм.
3. Размеры компенсаторов в комплекте.
Количество компенсаторов в комплекте соответствует числу ступеней компенсации.
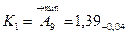
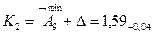
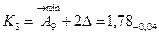
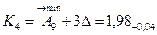
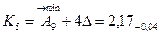
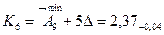
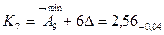
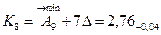
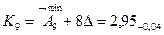
Дата добавления: 2017-04-05; просмотров: 6800;