Уравнение эвольвенты
Для получения уравнения эвольвенты обратимся к рис. 3.3. Положение произвольной точки Ay эвольвенты в полярной системе координат определяется двумя координатами относительно её начального радиус-вектора OA0 (или OC0): 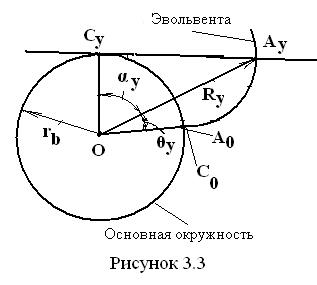 длиной радиус-вектора Ry и углом θy. Радиус-вектор Ry определим из прямоугольного треугольника OAyCy:
длиной радиус-вектора Ry и углом θy. Радиус-вектор Ry определим из прямоугольного треугольника OAyCy:
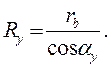
Для определения полярного угла θy сначала выразим длину дуги основной окружности через её радиус и центральный угол:
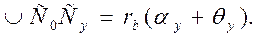
Выразим теперь противолежащий углу αy катет AyCy в ∆OAyCy:
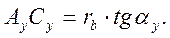
На основании четвёртого свойства эвольвенты имеем
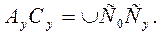
Подставляя в это равенство соответствующие выражения и решая его относительно θy, получаем
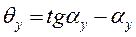 .
.
В этих математических выражениях и на рис. 3.3 угол αy называется профильным углом эвольвенты. Разность между тангенсом какого-либо угла и самим углом называется эвольвентной функцией и обозначается тремя первыми буквами латинского названия эвольвенты involute, т. е. inv, так что окончательно уравнение имеет вид:
θy = invαy.
В математических справочниках приводятся таблицы эвольвентной функции, в которых аргумент αy изменяется от нуля до нескольких десятков градусов.
Дата добавления: 2017-04-05; просмотров: 4624;











