Типовая схема эпициклического механизма

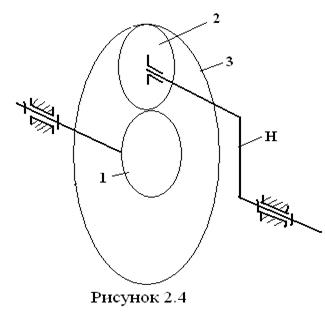На рис. 2.4 представлена одна из простейших типовых схем. Она включает центральное колесо 1 с внешними зубьями, называемое также солнечным колесом, центральное колесо 3 с внутренними зубьями и колесо 2, называемое сателлитом. Сателлит получил своё название из-за двух вращательных движений, в которых он участвует: вращения вокруг собственной оси и вращения вокруг общей оси механизма. Такую возможность ему предоставляет звено H стержневого типа, называемое водилом.

Если оба центральные колеса вращаются, то механизм имеет W = 2 и называется дифференциальным.

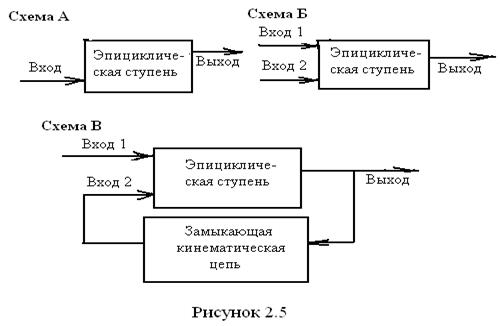
Если одно из центральных колёс заторможено, то W = 1, и механизм называется планетарным. Наиболее часто встречающиеся схемы механизмов планетарного типа в блочном представлении изображены на рисунке 2.5.

Схема А соответствует обыкновенному планетарному механизму, имеющему одно ведущее звено и одно ведомое при любом числе эпициклических ступеней. На схеме Б показана блок-схема дифференциального механизма с двумя ведущими и одним ведомым звеньями. На схеме В представлен так называемый механизм с замкнутым контуром, который составлен из одной или нескольких эпициклических ступеней, представляющих дифференциальную часть, и дополнительной кинематической цепи, соединяющей выходной вал механизма с одним из его входных валов. В результате такой связи в механизме остаётся одно ведущее и одно ведомое звенья.

Аналитический расчет кинематики

Для аналитического решения задач кинематики, при котором в дифференциальном механизме по заданным угловым скоростям ведущих звеньев определяется угловая скорость ведомого звена, а в планетарном механизме определяется передаточное отношение от ведущего звена к ведомому, применяют метод обращения движения. Он заключается в том, что всему механизму вместе со стойкой сообщается движение с угловой скоростью, равной и противоположно направленной угловой скорости водила. Тогда при сохранении характера относительного движения звеньев водило останавливается, а все звенья получают угловые скорости, уменьшенные на угловую скорость водила. Механизм в таком случае превращается в условный механизм с неподвижными осями колес. Это позволяет составить следующую таблицу скоростей:

№ звена	Угловые скорости звеньев в реальном механизме	Угловые скорости звеньев в механизме с условно неподвижным водилом
H	1 2 3 H	1(H)= 1 – H 2(H= 2 – H 3(H)= 3 – H H(H)= H – H =0

Записываем передаточное отношение от первого центрального колеса к третьему 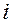₁₃^(H) при условно неподвижном водиле. Для схемы, представленной на рисунке 2.4, запишем 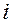₁₃^(H) _{= 1}^(H)⁄ ₃^(H), или после подстановки соответствующих разностей из таблицы получаем

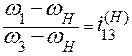. (а)

Из трех величин левой части две должны быть заданы, третья определяется решением данного уравнения.

В планетарном механизме, как сказано выше, одно из центральных колес неподвижно. Если принять колесо 3 с внутренними зубьями за неподвижное, т.е. принять ₃ = 0, то уравнение (а) запишется в виде 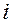₁₃^(H) ₌ ( ₁ ⁄ _H)/– _H . Разделив почленно числитель на знаменатель и заменив отношения угловых скоростей обозначениями передаточных отношений, получим окончательно:

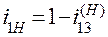, (б)

т. е. передаточное отношение в планетарном механизме от любого центрального колеса к водилу равно единице минус передаточное отношение от этого центрального колеса к другому центральному колесу в механизме с условно неподвижным водилом.

З а м е ч а н и е . При решении задачи кинематики одноступенчатого планетарного механизма (схема А по рис. 2.5) и одноступенчатого дифференциального механизма (схема Б по рис. 2.5) составляется и решается одно уравнение типа (б) или типа (а) соответственно. Если решается задача кинематики дифференциального механизма с замкнутым контуром (схема В по рис. 2.5), то необходимо составить два уравнения, одно из которых относится к дифференциальной ступени, другое – к замыкающей кинематической цепи, и решать эти уравнения как систему двух уравнений с двумя неизвестными.