Механизм с рядовым соединением колес
В этом механизме все колеса вращаются в одной плоскости, и каждое промежуточное колесо образует зацепление с двумя соседними (рис. 2.2).
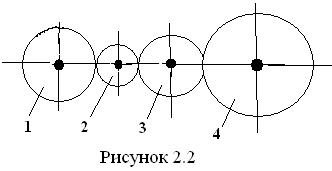 На схеме механизма цифрами обозначены номера колёс, а неподвижные оси затушёваны.
На схеме механизма цифрами обозначены номера колёс, а неподвижные оси затушёваны.
Согласно доказанному выше положению общее передаточное отношение данного механизма определяется равенством:
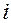 14 =
14 = 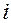 12 ·
12 · 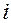 23·
23· 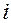 34.
34.
Записав передаточные отношения отдельных ступеней
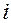 12 = –
12 = – 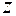 2/
2/ 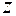 1,
1, 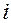 23 = –
23 = – 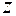 3/
3/ 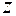 2 и
2 и 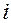 34 = –
34 = – 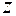 4/
4/ 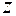 3
3
и подставив их в правую часть полученного ранее произведения, имеем
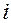 14 = (–
14 = (– 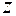 2/
2/ 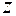 1)·(–
1)·(– 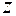 3/
3/ 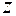 2)·(–
2)·(– 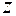 4/
4/ 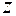 3),
3),
что после выполнения необходимых действий приводит к следующему результату
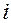 14 = –
14 = – 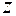 4/
4/ 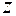 1.
1.
Этот результат показывает, что в механизмах такого типа передаточное отношение зависит только от чисел зубьев ведущего и ведомого колёс. Промежуточные колёса, числа зубьев которых не влияют на передаточное отношение, называются паразитными. Они позволяют только передать движение на небольшое расстояние и изменить его знак. Для общего случая механизма с произвольным числом колёс при вычислении передаточного отношения можно руководствоваться следующим выражением 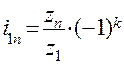 ,
,
где k – число внешних зацеплений, т. к. только они влияют на знак результата.
Дата добавления: 2017-04-05; просмотров: 1647;











