Эквивалентное определение ордерева.

Ордерево T — это конечное множество узлов, таких что: 1) Имеется один узел v, называемый корнем данного дерева; 2) Остальные узлы (исключая корень) содержатся в k попарно непересекающихся множествах.

Упорядоченные деревья.

Множества в эквивалентном определении ордерева являются поддеревьями.

Если относительный порядок поддеревьев фиксирован, то ордерево называется упорядоченным.

Представление в ЭВМ свободных, ориентированных и упорядоченных деревьев.

Обсуждению представлений деревьев можно предпослать в точности те же рассуждения, что были предпосланы обсуждению представлений графов (см. раздел 7.4). Кроме того, следует подчеркнуть, что задача представления деревьев в программе встречается гораздо чаще, чем задача представления графов общего вида, а потому методы ее решения оказывают еще большее влияние на практику программирования.

Представление свободных, ориентированных и упорядоченных деревьев.

Всякое свободное дерево можно ориентировать, назначив один из узлов корнем. Всякое ордерево можно произвольно упорядочить. Всякое упорядоченное дерево можно представить бинарным деревом, проведя правую связь к старшему брату, а левую - к младшему сыну.

Замечание:Рассматривается генеологическая терминология. Узлы, достижимые из узла называются потомками. Если в дереве существует дуга u, v, то узел u называют отцом, а узел v – сыном. Сыновья одного узла - братья

Пример: На рис. приведены диаграммы упорядоченного и соответствующего ему бинарного деревьев.

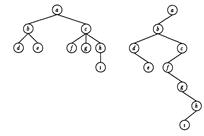
Таким образом, достаточно рассмотреть представление в ЭВМ бинарных деревьев.

Замечание: Из данного представления следует, что множество бинарных деревьев взаимнооднозначно соответствует множеству упорядоченных лесов упорядоченных деревьев.

Тема 16. Применение деревьев в программировании. Ассоциативная память. Выровненные деревья. Сбалансированные деревья. Минимальный каркас. Схема алгоритма построения минимального каркаса.

Ориентированные и упорядоченные ориентированные деревья интенсивно используются в программировании.

1. Выражения. Для представления выражений языков программирования, как правило, используются ориентированные упорядоченные деревья. Пример представления выражения а + b · с показан на рисунке слева.

2. Для представления блочной структуры программы и связанной с ней структуры областей определения идентификаторов часто используется ориентированное дерево (может быть, неупорядоченное, так как порядок определения переменных в блоке в большинстве языков программирования считается несущественным).

На рисунке в центре показана структура областей определения идентификаторов а, b, с, d, e, причем для отображения структуры дерева использована альтернативная техника.

3. Для представления иерархической структуры вложенности элементов данных и/или операторов управления часто используется техника отступов, показанная на рисунке справа.

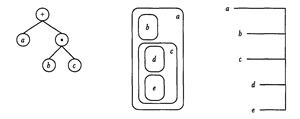
4. Структура вложенности каталогов и файлов в современных операционных систе-мах является упорядоченным ориентированным деревом.

5. Различные "уравновешенные скобочные структуры" (например (a(b)(c(d)(e)))) являются ориентированными упорядоченными деревьями.

Это отражается даже в терминологии – "корневой каталог диска".

Замечание: Общепринятой практикой при изображении деревьев является соглашение о том, что корень находится наверху и все стрелки дуг ориентированы сверху вниз, поэтому стрелки можно не изображать. Таким образом, диаграммы свободных, ориентированных и упорядоченных деревьев оказываются графически неотличимыми, и требуется дополнительное указание, дерево какого класса изображено на диаграмме. В большинстве случаев это ясно из контекста.

Пример: На рис. 8.8 приведены три диаграммы деревьев, которые внешне выглядят раз­личными. Обозначим дерево слева – (1), в центре – (2) и справа – (3). Как упорядоченные деревья, они все различны: (1) ^ (2), (2) ^ (3), (3) ^ (1). Как ориентированные деревья (1) = (2), но (2) ^ (3). Как свободные деревья, они все изоморфны: (1) = (2) = (3).