Теорема Форда - Фалкерсона. Алгоритм нахождения максимального потока.

Теорема:На любой сети максимальная величина потока из истока S в сток t равна минимальной пропускной способности разреза, отделяющего S от t. Т.е. существует такой поток по сети:M*G =max∑Mi = minC(A/B).

Алгоритм нахождения максимального потока:1) Построить некоторый начальный поток X0 = {X0ij}. В примере это потоки М1 и М2.2) Организовать процедуру составления подмножества А вершин, достижимых из истока S по ненасыщенным ребрам. А={s, 3, 2, t}. Если в этом процессе сток t не попадает в подмножество А, то построенный поток максимальный и задача решена, если же сток t попал в А, то перейти к пункту 3 алгоритма. 3) Выделить путь из истока s в сток t, состоящий из ненасыщенных ребер и увеличить поток Хij по каждому ребру этого пути на величину ∆=min(Cij-Xij), где min берется по i-тым j-тым ребрам этого пути. Тем самым будет построен поток и затем следует вернуться к пункту 2 алгоритма. ( Мы построили М3 ). А={1}, В={2, 3, 4, 5}. R*(A/B)=6.

Тема 14. Кратчайшие пути. Алгоритм Флойда. Алгоритм Дейкстры.

Если задан орграф G(V, E), в котором дуги помечены числами и эти числа обычно называют весами или длинами, то орграф можно представить в виде матрицы весов.

||Cij|| =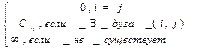

Длиной пути называется сумма длин дуг, входящих в этот путь. Наиболее часто на практике встречается задача отыскания кратчайшего пути. Алгоритм Флойда находит все кратчайшие пути между всеми парами вершин в орграфе. Алгоритм ДХ3 находит кратчайший путь между двумя данными вершинами орграфа, если длины дуг неотрицательны.

Кратчайшие пути

Ориентированный граф G = (V, E) состоит из множества вершин V и множества дуг E. Вершины также называют узлами, а дуги – ориентированными ребрами. Дуга представима в виде упорядоченной пары вершин (v, w), где вершина v называется началом, а w – концом дуги.

Неориентированный граф G = (V, E) состоит из конечного множества вершин V и множества ребер E. В отличие от ориентированного графа, здесь каждое ребро (v, w) соответствует неупорядоченной паре вершин: если (v, w) – неориентированное ребро, то (v, w) = (w, v).

Вершина Х называется инцидентной ребру G, если ребро соединяет эту вершину с какой-либо другой вершиной.

В задаче о кратчайшем пути нам дан ориентированный взвешанный граф G = (V, E) с вещественной весовой функцией w: E 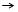R

Вес пути p=(v₀,v₁,...,v_k) - это сумма весов рёбер, входящих в этот путь:

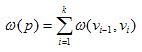
Вес кратчайшего путииз u в v равен, по определению,

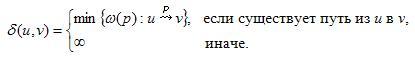
Кратчайший путь из u в v - это любой путь p из u в v, для которого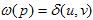

Граф называется вырожденным, если у него нет рёбер.

Вершины называются смежными, если существует ребро, их соединяющее.

Пустым называется граф без рёбер. Полным называется граф, в котором каждые две вершины смежные.

Цикл, в котором все вершины, кроме первой и последней, попарно различны, называется простым циклом.

Граф называется связным, если для любых двух вершин существует путь, соединяющий эти вершины.