Свободные деревья. Основные свойства деревьев.

Деревья заслуживают отдельного и подробного рассмотрения по двум причинам.

Деревья являются в некотором смысле простейшим классом графов. Для них вы-полняются многие свойства, которые не всегда выполняются для графов в общем случае. Применительно к деревьям многие доказательства и рассуждения оказываются намного проще. Выдвигая какие-то гипотезы при решении задач теории графов, целесообразно сначала их проверять на деревьях.

Деревья являются самым распространенным классом графов, применяемых в про-граммировании, причем в самых разных ситуациях. Более половины объема этой главы посвящено рассмотрению конкретных применений деревьев в программировании.

Свободные деревья. Изучение деревьев целесообразно начать с самых общих определений и установления основных свойств. Граф без циклов называется ациклическим, или лесом. Связный ациклический граф называется (свободным) деревом. Таким образом, компонентами связности леса являются деревья. Замечание: Прилагательное "свободное" употребляется в том случае, когда нужно подчеркнуть отличие деревьев от других объектов, родственных деревьям: ориентированных деревьев, упорядоченных деревьев и т. д.

В связном графе G выполняется неравенство q(G) ³ p(G) – 1. Граф G, в котором q(G) = p(G) – 1, называется древовидным. В ациклическом графе G z(G) = 0 Пусть и, v — несмежные вершины графа G, х = (u,v) 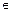E. Если граф G + х имеет только один простой цикл, z(G + х) = 1, то граф G называется субциклическим.

Пример:

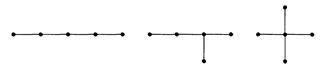
На рисунке показаны диаграммы всех различных (свободных) деревьев с 5 вер­шинами.

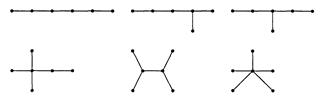
На рисунке - диаграммы всех различных (свободных) деревьев с 6 вершинами

Основные свойства деревьев. Следующая теорема устанавливает, что два из четырех свойств – связность, ацикличность, древовидность и субцикличность – характеризуют граф как дерево.

Теорема:Пусть G(V, Е) – граф с р вершинами, q ребрами, k компонентами связности и z простыми циклами. Пусть далее х – ребро, соединяющее любую пару несмежных вершин в графе G, тогда следующие утверждения эквивалентны:

1. Граф G - дерево, то есть связный граф без циклов k(G) = 1 & z(G) = 0 ;

2. Любые две вершины соединены в G единственной простой цепью: G: "u,v $ ! <u, v>;

3. Граф G - связный граф, и любое ребро есть связный мост G: k(G) = 1 & "e Î Ek(G – e) > 1;

4. Граф G - связный и древовидный G: k(G) = 1 & q(G) = p(G) – 1;

5. Граф G - ациклический и древовидный G: z(G) = 0 & q(G) = p(G) – 1;

6. Граф G - ациклический и субциклический G: z(G) = 0 & z(G + x) = 1;

7. Граф G - связный, субциклический и неполный.

Следствие: В любом нетривиальном дереве имеются по крайней мере две висячие вершины.