Уравнения равновесия твёрдого тела

Пусть О – начало координат; 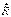– результирующая сила; 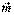– момент результирующей пары. Пусть точка О1 – новый центр приведения (рис.15).

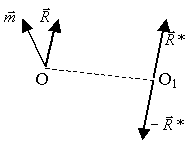
Рис.15.

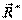и : .

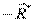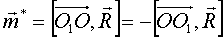Новая система сил:

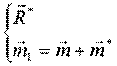
Заметим:

.

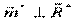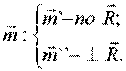
При изменении точки приведения => меняется только 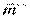(в одну сторону с одним знаком, в другую – с другим). То есть 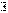точка: 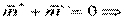совпадают лини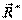и и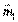

Аналитически: 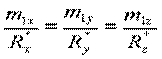(колинеарность векторов)

Или: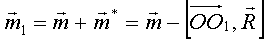

; координаты точки О1.

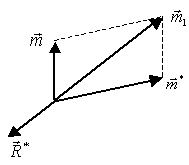
Рис.16.

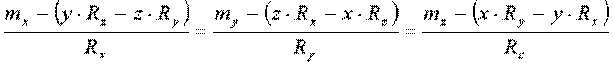
Это уравнение прямой линии, для всех точек которой направление результирующего вектора совпадает с направлением момента результирующей пары – прямая называется динамой.

Если на оси динамы => 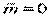, то система эквивалентна одной результирующей силе, которую называют равнодействующей силой системы. При этом всегда 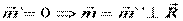, то есть .

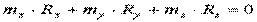Четыре случая приведения сил:

1.) 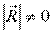; 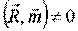- динама.

2.) 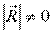; 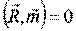- равнодействующая.

3.) 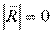; 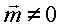- пара.

4.) 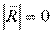; 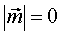- равновесие.

Два векторных уравнения равновесия: главный вектор и главный момент равны нулю , .

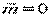Или шесть скалярных уравнений в проекциях на декартовые оси координат:

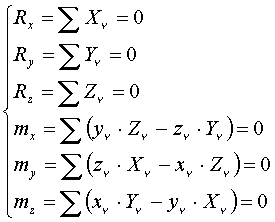
Здесь: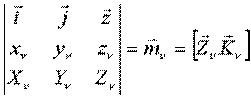

Сложность вида уравнений зависит от выбора точки приведения => искусство расчётчика.

Нахождение условий равновесия системы твёрдых тел, находящихся во взаимодействии <=> задача о равновесии каждого тела в отдельности, причём на тело действуют внешние силы и силы внутренние (взаимодействие тел в точках соприкосновения с равными и противоположно направленными силами – аксиома IV, рис.17).

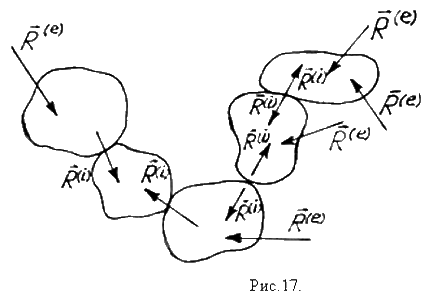
Выберем для всех тел системы один центр приведения. Тогда для каждого тела с номером 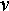условия равновесия:

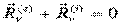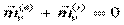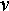, , ( = 1, 2, …, k)

где 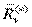, 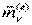- результирующая сила и момент результирующей пары всех сил, кроме внутренних реакций.

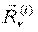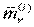, - результирующая сила и момент результирующей пары сил внутренних реакций.

Формально суммируя по 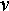и учитывая по IV аксиоме

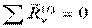
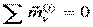
получаем необходимые условия равновесия твёрдого тела:

,

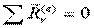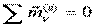
Пример.

Равновесие: = ?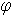

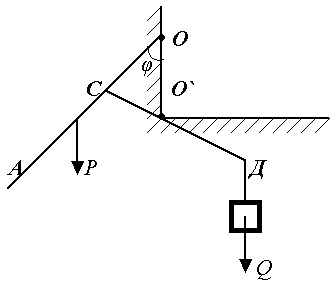
Рис.18.

Контрольные вопросы:

1. Назовите все случаи приведения системы сил к одной точке.

2. Что такое динама?

3. Сформулируйте необходимые условия равновесия системы твёрдых тел.