Структура теоретической механики. Основы статики

В теоретической механике изучается движение тел относительно других тел, представляющие собой физические системы отсчёта.

Механика позволяет не только описывать, но и предсказывать движение тел, устанавливая причинные связи в определённом, весьма широком, круге явлений.

Основные абстрактные модели реальных тел:

1. материальная точка– имеет массу, но не имеет размеров;
2. абсолютно твёрдое тело – объём конечных размеров, сплошь заполненный веществом, причём расстояния между любыми двумя точками среды, заполняющей объём, не изменяются во время движения;
3. сплошная деформируемая среда– заполняет конечный объём или неограниченное пространство; расстояния между точками такой среды могут меняться.

Из них – системы:

- система свободных материальных точек;

- системы со связями;

- абсолютно твёрдое тело с полостью, заполненной жидкостью, и т.п.

«Вырожденные» модели:

- бесконечно тонкие стержни;

- бесконечно тонкие пластины;

- невесомые стержни и нити, связывающие между собой материальные точки, и т.д.

Из опыта: механические явления протекают неодинаково в разных местах физической системы отсчёта. Это свойство – неоднородность пространства, определяемого физической системой отсчёта. Под неоднородностью здесь понимается зависимость характера протекания явления от места, в котором мы наблюдаем это явление.

Ещё свойство – анизотропность (неизотропность) движение тела относительно физической системы отсчёта может быть различным в зависимости от направления. Примеры: течение реки по меридиану (с севера на юг - Волга); полёт снаряда, маятник Фуко.

Свойства системы отсчёта (неоднородность и анизотропность) затрудняют наблюдение за движением тела.

Практически свободна от этого – геоцентрическая система: центр системы в центре Земли и системы не вращается относительно «неподвижных» звёзд). Геоцентрическая система удобна для расчётов движений на Земле.

Для небесной механики (для тел солнечной системы): гелиоцентрическая система отсчёта, которая движется с центром масс Солнечной системы и не вращается относительно «неподвижных» звёзд. Для этой системы пока не обнаружены неоднородность и анизотропность пространства

по отношению к явлениям механики.

Итак, вводится абстрактная инерциальная система отсчёта, для которой пространство однородно и изотропно по отношению к явлениям механики.

Инерциальная система отсчёта – такая, собственное движение которой не может быть обнаружено никаким механическим опытом. Мысленный эксперимент: «точка, одинокая во всём мире» (изолированная) либо покоится, либо движется прямолинейно и равномерно.

Все системы отсчёта движущиеся относительно исходной прямолинейно, равномерно будут инерциальными. Это позволяет ввести единую декартовую систему координат. Такое пространство называется евклидовым.

Условное соглашение – берут правую систему координат (рис. 1).

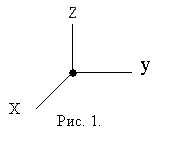Время – в классической (нерелятивистской) механике абсолютно, единое для всех систем отсчёта то есть начальный момент – произволен. В отличие релятивистской механики, где применяется принцип относительности.

Состояние движения системы в момент времени t определяется координатами и скоростями точек в этот момент.

Реальные тела взаимодействуют при этом возникают силы, которые меняют состояние движения системы. Это и есть суть теоретической механики.

Как изучается теоретическая механика?

1. Учение о равновесии совокупности тел некоторой системы отсчёта – раздел статика.
2. Раздел кинематика: часть механики, в которой изучаются зависимости между величинами, характеризующими состояние движения систем, но не рассматриваются причины, вызывающие изменение состояния движения.

После этого рассмотрим влияние сил [ОСНОВНАЯ ЧАСТЬ].

1. Раздел динамика: часть механики, в которой рассматривается влияние сил на состояние движения систем материальных объектов.

Принципы построения основного курса – динамики:

1) в основе – система аксиом (на основе опыта, наблюдений);

2) далее – законы внутренней логики (относительная независимость теории).

Постоянно – безжалостный контроль практики.Признак точной науки – наличие внутренней логики (без неё - набор не связанных рецептов)!

Статикой называется та часть механики, где изучаются условия, которым должны удовлетворять силы, действующие на систему материальных точек, для того чтобы система находилась в равновесии, и условия эквивалентности систем сил.

Будут рассмотрены задачи о равновесии в элементарной статике с применением исключительно геометрических методов, основанных на свойствах векторов. Такой подход применяется в геометрической статике (в отличие от аналитической статики, которая здесь не рассматривается).

Положения различных материальных тел будем относить к системе координат, которую примем за неподвижную.

Идеальные модели материальных тел:

1) материальная точка – геометрическая точка с массой.

2) абсолютно твёрдое тело – совокупность материальных точек, расстояния между которыми не могут быть изменены никакими действиями.

Силами будем называть объективные причины, являющиеся результатом взаимодействия материальных объектов, способные вызвать движение тел из состояния покоя или изменить существующее движение последних.

Так как сила определяется вызываемым ею движением, то она также имеет относительный характер, зависящий от выбора системы отсчёта.

Вопрос о природе сил рассматривается в физике.

Система материальных точек находится в равновесии, если, будучи в покое, она не получает никакого движения от сил, на неё действующих.

Из повседневного опыта: силы имеют векторный характер, то есть величину, направление, линию действия, точку приложения. Условие равновесия сил, действующих на твёрдое тело, сводится к свойствам систем векторов.

Обобщая опыт изучения физических законов природы, Галилей и Ньютон сформулировали основные законы механики, которые могут рассматриваться как аксиомы механики, так как имеют в своей основе экспериментальные факты.

Аксиома 1. Действие на точку твёрдого тела нескольких сил равносильно действию одной равнодействующей силы, строящейся по правилу сложения векторов (рис.2).

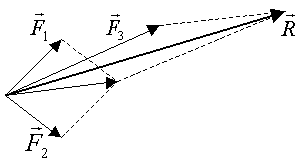
Рис.2.

Следствие.Силы, приложенные к точке твёрдого тела, складываются по правилу параллелограмма.

Аксиома 2. Две силы, приложенные к твёрдому телу, взаимно уравновешиваются тогда и только тогда, когда они равны по величине, направлены в противоположные стороны и лежат на одной прямой.

Аксиома 3. Действие на твёрдое тело системы сил не изменится, если добавить к этой системе или отбросить от неё две силы, равные по величине, направленные в противоположные стороны и лежащие на одной прямой.

Следствие. Силу, действующую на точку твёрдого тела, можно переносить вдоль линии действия силы без изменения равновесия (то есть, сила является скользящим вектором, рис.3)

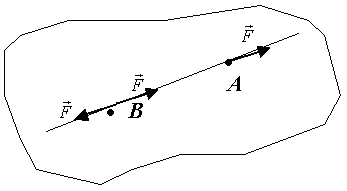
Рис.3.

Две категории сил.

1) Активные – создают или способны создать движение твёрдого тела. Например, сила веса.

2) Пассивные – не создающие движения, но ограничивающие перемещения твёрдого тела, препятствующие перемещениям. Например, сила натяжения нерастяжимой нити (рис.4).

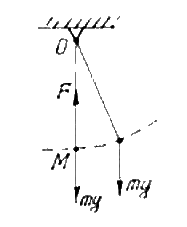
Рис.4.

Аксиома 4. Действие одного тела на второе равно и противоположно действию этого второго тела на первое (действие равно противодействию).

Геометрические условия, ограничивающие перемещение точек, будем называть связями.

Условия связи: например,

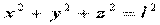- стержень непрямой длины l.

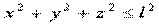- гибкая нерастяжимая нить длиной l.

Силы, обусловленные связями и препятствующие перемещениям, называются силами реакций.

Аксиома 5. Связи, наложенные на систему материальных точек, можно заменить силами реакций, действие которых эквивалентно действию связей.

Когда пассивные силы не могут уравновесить действие активных сил, начинается движение.

Две частные задачи статики

1. Система сходящихся сил, действующих на твёрдое тело

Системой сходящихся сил называется такая система сил, линии действия которой пересекаются в одной точке, которую всегда можно принять за начало координат (рис.5).

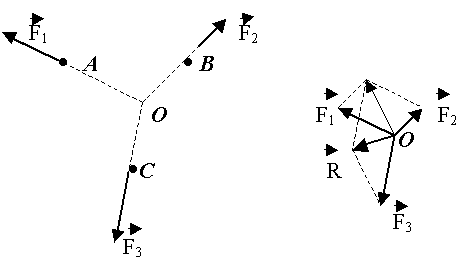
Рис.5.

Проекции равнодействующей:

;

;

.

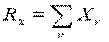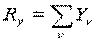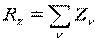Если 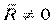, то сила вызывает движение твёрдого тела.

Условие равновесия для сходящейся системы сил:

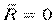
	или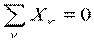

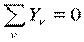
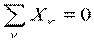
2. Равновесие трёх сил

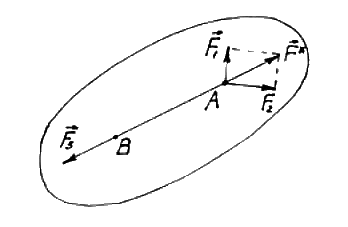
Рис.6.

Если на твёрдое тело действуют три силы, и линии действия двух сил пересекаются в некоторой точке А, равновесие возможно тогда и только тогда, когда линия действия третьей силы тоже проходит через точку А, а сама сила 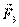равна по величине и противоположно направлена сумме 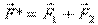(рис.6).

Примеры:

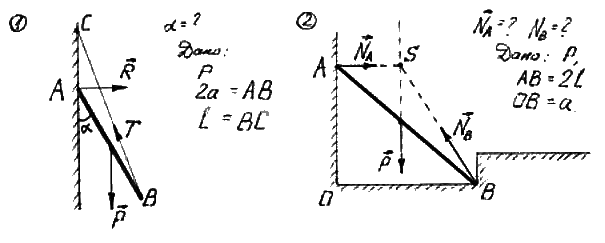
Рис.7.		Рис.8.

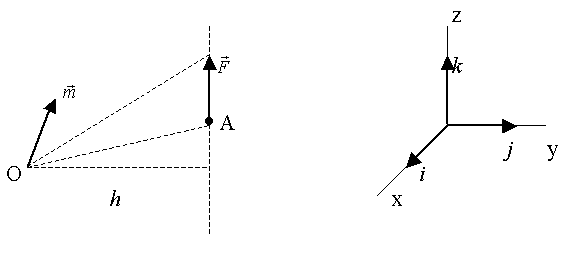
Рис.9.

Момент силы 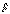относительно точки О определим как вектор 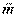, по величине равный удвоенной площади треугольника, основанием которого является вектор силы 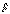с вершиной в заданной точке О; направление – ортогонально плоскости рассмотренного треугольника в ту сторону, откуда вращение, производимое силой 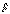вокруг точки О, видно против хода часовой стрелки. 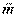является моментом скользящего вектора и является свободным вектором (рис.9).

Итак: 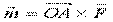или

,

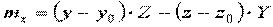
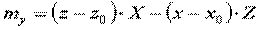
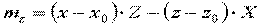
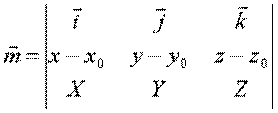где ; ; .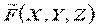

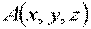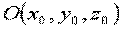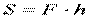, где F – модуль силы, h – плечо (расстояние от точки до направления силы).

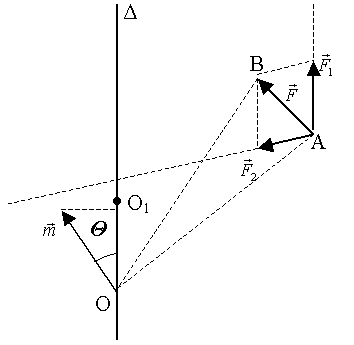
Рис.10.

Моментом силы 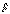относительно оси 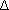называется алгебраическое значение проекции на эту ось вектора момента силы 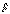относительно произвольной точки О, взятой на оси 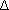(рис.10).

Это скаляр, не зависящий от выбора точки. Действительно, разложим 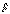: 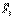|| 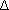и 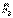в плоскости .

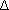О моментах: пусть О₁ – точка пересечения 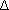с плоскостью 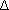. Тогда:

а) от 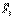- момент 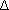=> проекция = 0.

б) от 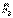- момент вдоль 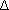=> является проекцией.

Итак, момент относительно оси – это момент составляющей силы в перпендикулярной плоскости к оси относительно точки пересечения плоскости и оси.

Теорема Вариньона для системы сходящихся сил:

Момент равнодействующей силы для системы сходящихся сил относительно произвольной точки А равен сумме моментов всех составляющих сил относительно той же точки А (рис.11).

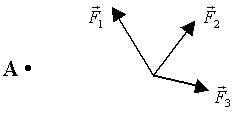
Рис.11.

Доказательство в теории сходящихся векторов.

Пояснение: сложение сил по правилу параллелограмма => результирующая сила даёт суммарный момент.

Контрольные вопросы:

1. Назовите основные модели реальных тел в теоретической механике.

2. Сформулируйте аксиомы статики.

3. Что называется моментом силы относительно точки?