Пример расчета (задача № 13)

Дан пространственный консольный брус с ломаным очертани­ем осевой линии, нагруженный сосредоточенной силой Р = 1 кН и равномерно распределенной нагрузкой q = 2 кН/м. На рис. 5.34, а этот брус показан в аксонометрии в соответствии с прямоугольной системой координат xyz . Вертикальный элемент бруса имеет попе­речное сечение в виде круга диаметром d = 0,06 м (рис. 5.34, в), горизонтальные элементы бруса имеют поперечные сечения в виде прямоугольника (рис. 5.34, б). Ширина сечения b = d = 0,06 м, а высота сечения c = 0,5 d = 0,03 м. Ориентация главных осей попе­речных сечений на каждом участке показана на рис. 5.34, г.

Требуется:

1. Построить в аксонометрии эпюры M_x , M_y , M_z , N_z, Q_x , Q_y ;

2. Указать вид сопротивления для каждого участка бруса;

3. Определить максимальные напряжения в опасном сечении каждого участка от внутренних усилий N_z, M_x , M_y и M_z (касатель­ными напряжениями от Q_x и Q_y можно пренебречь);

4. Проверить прочность при расчетном сопротивлении R = = 180 МПа.

Решение

1. Построить в аксонометрии эпюры M_x , M_y , M_z , N_z, Q_x , Q_y . Заметим, что так как заданная система пространственная, при произвольном характере нагружения, в опорном сечении, где установлена заделка, возникает шесть опорных реакций (три опор­ные силы и три момента). Для определения опорных реакций, в данном случае, можем применить шесть уравнений равновесия ста­тики. Так как число независимых уравнений равновесия равно чис­лу опорных реакций, то можно сделать вывод, что рассматриваемая система в виде ломаного бруса, с заделанным одним концом, явля­ется статически определимой. Поэтому рассматриваемая система разрешима по методу сечений. Далее, учитывая особенности конст­рукции, определение величин внутренних усилий можно осущест­вить без предварительного вычисления величин опорных реакций.

6. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ
СИСТЕМ МЕТОДОМ СИЛ

6.1. Стержневые системы.
Степень статической неопределимости

Под стержневой системой понимается всякая конструк­ция, состоящая из элементов, имеющих форму бруса. Если эле­менты конструкции работают только на растяжение или сжатие си­стема называется фермой (рис. 6.1). Ферма состоит из шарнирно опертых между собой прямых стержней, образующих треугольники и для нее характерно приложение внешних сил в узлах заданной системы.

Если элементы стержней системы работают в основном на изгиб или кручение, то такая система называется рамой (рис. 6.2).

Если все элементы стержневой системы расположены в одной плоскости, в которой также действуют все внешние силы, включая реакции опор, то система называется плоской (рис. 6.1, 6.2).

Если все элементы заданной системы расположены в одной плоскости, а внешние силы действуют в перпендикулярной плос­кости, то система называется плоскопространственной (рис. 6.3). Стержневые системы, не относящиеся к двум указанным категориям, называются пространственными (рис. 6.4).

Все стержневые системы принято разделять на статически определимые и статически неопределимые. Под статически определимой понимается такая система, для которой усилия во всех ее элементах могут быть определены по методу сечений с применением лишь урав­нений равновесия. Если этого сделать нельзя, то такая система на­зывается статически неопределимой.

Разность между числом неизвестных усилий (реакций опор и внутренних силовых факторов) и числом независимых уравнений равновесий, которые могут быть составлены для рассматриваемой сис­темы, называется степенью статической неопредели­мости системы.

Связи, наложенные на систему, бывают внешними и внутрен­ними. Под внешними понимают ограничения, накладываемые на абсолютные перемещения точек системы, как единое целое. Внутренние же связи ограничивают взаимные (относительные) перемещения элементов системы. Следовательно, статическая неопределимость системы мо­жет быть вызвана как внешними, так и внутренними связями.

Если рассматривать внешние связи, то можно отметить, что по­ложение жесткого тела на плоскости x,y характеризуется тремя незави­симыми параметрами - координатами x, y и углом поворота рассматриваемой плоскости. Таким образом, необходимое для равновесия число наложен­ных внешних связей должно быть равно трем (по количеству уравнений равновесия - åx = 0, åy = 0, åm = 0). Если плоская система состоит из D частей, каждую из которых можно рассмат­ривать как жесткое тело, то количество параметров, определяющих положение этой системы будет равно 3 D. Каждый шарнир, соеди­няющий две части системы, разрешает лишь их взаимный поворот, устраняя возможность их взаимных смещений - следовательно он уменьшает количество возможных перемещений системы на две единицы. Кроме этого, каждый опорный стержень устраняет воз­можность перемещения системы в соответствующем направлении. Таким образом, подсчитать степень статической неопределимости системы, определяемую внешними связями, можно по следующей формуле:

W = 3 D - 2 Ш - С,

где D - число частей (“дисков”) системы, каждая из которых может рассматриваться как абсолютно жесткое тело, Ш - количество шар­ниров в системе, соединяющих “диски”, С - число опорных стерж­ней. Для статически определимых систем W =0. При W<0 система является статически неопределимой.

Наиболее характерные типы внешних связей и их схематичные изображения рассмотрены в п. 5.1.

На рис. 6.5 показана плоская рама, имеющая в первом (а) случае три внешние связи, а во втором случае (б) - пять. Значит, в первом случае рама имеет необходимое для статической определи­мости количество внешних связей, а во втором же - две дополни­тельные внешние связи. Однако в обеих ситуациях рама статически неопределима, т.к. конфигурация ее такова, что не позволяет опре­делить усилия во всех ее элементах, используя только уравнения равновесия. Следовательно, для окончательного ответа на вопрос о статической определимости системы необходимо проведение сов­местного анализа наложенных на систему внешних и внутренних связей (более подробно этот вопрос рассматривается в курсе строи­тельной механики).

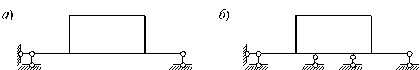
Рис. 6.5

Методы расчета статически неопределимых систем основаны на определении перемещений в ее точках. Выше мы рассматривали метод начальных параметров для вычисления перемещений в бал­ках. При всех достоинствах этого метода он обладает одним суще­ственным недостатком - при большом количестве участков вычис­лительные формулы становятся весьма громоздкими. Особенно это существенно в случае криволинейной оси стержневой системы.

В связи с этим, рассмотрим более универсальный метод опре­деления перемещений - метод Мора, названный так по имени немецкого ученого, предложившего его.