Пример расчета (задача № 4)

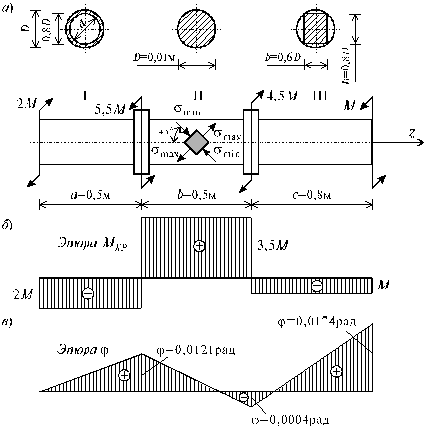
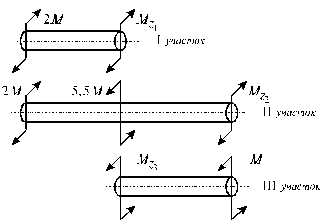
Стальной валик переменного сечения, испытывающего круче­ние, закручивается крутящими моментами, действующими в двух крайних и двух пролетных сечениях. Расчетная схема валика, ее геометрические размеры, величины и точки приложения внешних крутящих моментов указаны на рис. 4.4, а.

Требуется:

1. Построить эпюру крутящих моментов;

2. Найти допускаемую величину момента М;

3. Построить эпюры касательных напряжений по сечениям вала, отметив на сечениях опасные точки;

4. Построить эпюру углов закручивания;

Модуль упругости при сдвиге материала вала G = 8×10⁷ кН/м². Расчетное сопротивление материала вала срезу R_C = 10⁵ кН/м².

Решение

1. Построить эпюру крутящих моментов. Для опре­деления величины крутящих моментов используется метод сечений. Согласно расчетной схемы (рис. 4.5, а) для I участка (0 £ z £ 0,5 м):

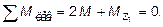откуда .

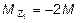Согласно расчетной схемы (рис. 4.5, б) для участка II (0,5 м £ £ z £ 1,0 м):

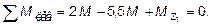откуда .

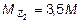Согласно расчетной схемы (рис. 4.5, в) для участка III (1,0 м £ £ z £ 1,8 м):

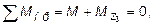откуда .

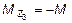По полученным данным строим эпюру крутящих моментов (рис. 4.4, б).

2. Найти допускаемую величину момента М. Допус­каемая величина момента М_P определяется из условия прочности:

.

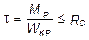Рис. 4.4

Сначала определим моменты сопротивления сечения валика для каждого участка.

I участок (трубчатое сечение) согласно (4.13):

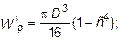где ;

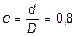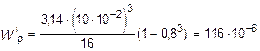м³.

II участок (круглое сечение):

Рис. 4.5

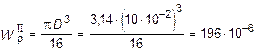м³.

III участок (прямоугольное сечение):

,

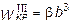где b - коэффициент, зависящий от отношения сторон прямоуголь­ного сечения h/b (h > b). В данном случае 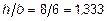, 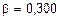тогда

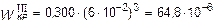м³.

Подсчитаем теперь напряжения по участкам в зависимости от момента М:

.

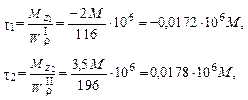
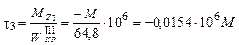Из сравнения результатов видно, что наиболее напряженным является участок II, поэтому допускаемая величина момента [M] определяется из зависимости:

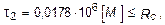
откуда

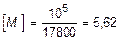кН×м.

4. Построить эпюры касательных напряжений по сечениям вала, отметив на сечениях опасные точки. Касательные напряжения в точках поперечного сечения валика определяются по формулам:

для круглого сечения при 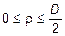, t ;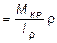

для трубчатого сечения при 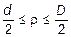, t ;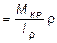

для прямоугольного сечения 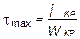(в середине большей стороны) и t₁ = g t_max (в середине меньшей стороны).

Подсчитаем моменты инерции сечений валика относительно центра их кручения.

Участок I (трубчатое сечение):

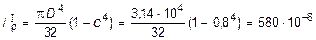м⁴.

Участок II (круглое сечение):

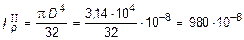м⁴.

Участок III (прямоугольное сечение):

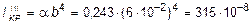м⁴,

где a = 0,243 при h/b = 1/33.

Определим значения напряжений в характерных точках сече­ний.

Участок I (0 £ z £ 0,5 м):

при 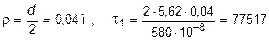кН/м² = 77,5 МПа;

при 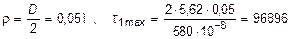кН/м² =97,0МПа.

Участок II ( 0,5 м £ z £ 1,5 м):

при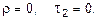

при 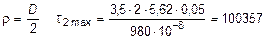кН/м² = 100,0 Мпа.

Участок III (1,0 м £ z £ 1,8 м): в середине большей стороны

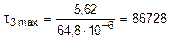кН/м² = 86,8 МПа,

в середине меньшей стороны

t₃ = g t_max = 0,906×86,7 = 78,6 МПа.

где g = 0,906 при h/b = 1,33.

По полученным данным строятся эпюры напряжений, приведенные на рис. 4.6.

4. Построить эпюру углов закручивания. Угол за­кручивания на i-ом участке вала в соответствии с (4.10) опре­деляется:

,

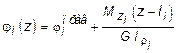где 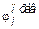- угол закручивания на правом конце (i-1)-го участка (для первого участка 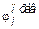- начальный угол закручивания вала); l_i - координата начала i-го участка.

Рис. 4.6

Так как, в данном случае в пределах каждого из трех участков крутящие моменты и жесткости на кручение GI_r постоянны, то эпюры углов закручивания на каждом из участков будут линейны. В связи с этим, достаточно подсчитать их значения лишь на границах участков. Приняв, что левый конец вала защемлен от поворота, т.е. j (0) = 0, получим:

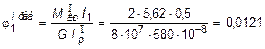рад;

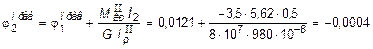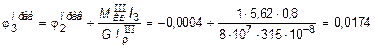рад;

рад.

По полученным данным строим эпюру углов закручивания j (рис. 4.4, в). Сравнивая эпюры t и j, можно отметить очевидную закономерность их изменения по оси z, вытекающую из расчетных формул.

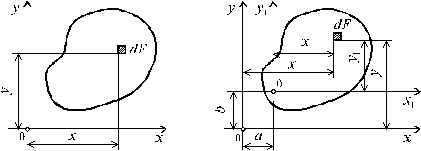Рис. 3.1 Рис. 3.2

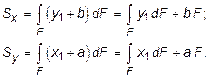(3.3)

Величины а и b можно подобрать (причем единственным обра­зом) так, чтобы выполнялись следующие равенства:

b×F = S_x ; a×F = S_y , (3.4)

тогда статические моменты .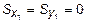

Ось, относительно которой статический момент равен нулю, называется центральной. Точка С (x_C , y_C) пересечения централь­ных осей называется центром тяжести сечения в системе координат (x, y) и определяется из (3.4):

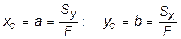. (3.5)

Далее предположим, что брус имеет составное сечение (рис. 3.3) с общей пло­щадью F. Обозначим через F_k (k = 1, 2, 3,..., n) площадь k-ой области, принадлежащей к составному сечению бруса. Тогда выраже­ние (3.1) можно преобразовать в следующем виде:

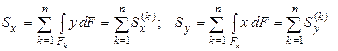, (3.6)

где 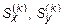- статические моменты k-той области относительно осей x и y. Следовательно, статический момент составного сечения равен сумме статических моментов составляющих областей.