Схема III. Плоская рама (задача № 8)
Заданная плоская стержневая система (рис. 5.17, а), элементы которой представляют собой прямолинейные стержни, жестко соединенных между собой, называется рамой. При произвольном характере нагружения, в поперечных сечениях элементов заданной системы возникают следующие три силовых фактора: поперечная сила Q, изгибающий момент M и продольная сила N. Главной отличительной особенностью рамной системы от других стержневых систем является то, что в деформированной состоянии угол сопряжения между различными элементами равен углам сопряжения элементов до нагружения системы.
Правило знаков для Qy , Mx и Nz и порядок построения их эпюр для таких систем остаются прежними.
Так как заданная система имеет только три внешние связи (вертикальную и горизонтальную в т. D и горизонтальную в т. А), следовательно, при общем характере нагружения возникает всего три опорные реакции. Как нам уже известно, для плоских систем можно воспользоваться только тремя уравнениями равновесия статики для определения опорных реакций, поэтому заданная система является статически определимой.

|
Рис. 5.17
Построить эпюры Qy, Mx и Nz.
Определение опорных реакций. Составив уравнения равновесия для всей рамы и решив их, получим:
Sy = 0, RD = 0;
SMD = 0, -HA ×8 + Р×4 + q×4×2 = 0, 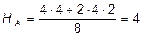 кН;
кН;
SMA = 0, HD ×8 - Р×4 - q×4×6 = 0, 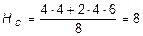 кН.
кН.
Проверка: Sx = 0; HA + HD - Р - q×4 = 0;
4 + 8 - 4 - 2×4 = 0; 12 - 12 = 0; 0 = 0.
Уравнение равновесия превращается в тождество, что говорит о правильности вычисления опорных реакций.
Определение количества участков
Так как, в рамах границами участков являются точки приложения сил и точки изменения направления оси элементов системы, то заданная система имеет три участка: участок I - АВ, участок II -ВС, участок III - СD (рис. 5.13, б).
Составление аналитических выражений Qy, Mx и Nz и определение их значений в характерных сечениях каждого участка
Определение внутренних силовых факторов в сечениях рам производится также с помощью метода сечений. Однако при выполнении разрезов всегда следует выяснить, какую из частей рамы считать левой, а какую правой. Для этого предполагают, что обход рамы ведется слева направо, т.е. от А к В, от В к С, от С к D. При этом наблюдение ведут с нижней стороны участков, находясь лицом к оси участков.
Участок I (0 £ z1 £ 4 м) (рис. 5.18).
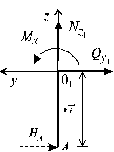 Рис. 5.18
Рис. 5.18
|
Проведя сечение в пределах этого участка, рассмотрим равновесие левой отсеченной части длиной z1 . Составив уравнение равновесия Sy = 0 и 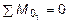 и Sz = 0 для этой части и решив их относительно
и Sz = 0 для этой части и решив их относительно 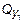 ,
, 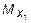 и
и 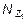 , получим аналитические выражения изменения Qy , Mx и Nz на участке I:
, получим аналитические выражения изменения Qy , Mx и Nz на участке I:
Sy = 0, -HA - 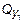 =0,
=0, 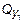 = - HA - const;
= - HA - const;
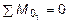 , - HA×z1 -
, - HA×z1 - 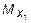 = 0,
= 0, 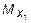 = - HA×z1 -уравнение прямой;
= - HA×z1 -уравнение прямой;
Sz = 0, 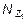 = 0 - нормальная сила отсутствует.
= 0 - нормальная сила отсутствует.
Величины Qy , Mx и Nz в граничных сечениях участка будут равны:
при z1 = 0 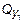 = -4 кН,
= -4 кН, 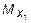 = 0,
= 0, 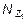 = 0;
= 0;
при z1 = 4 м 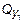 = -4 кН,
= -4 кН, 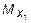 = -4×4 = -16кН×м,
= -4×4 = -16кН×м, 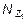 = 0.
= 0.
Участок II (0 £ z2 £ 4 м) (рис. 5.19).
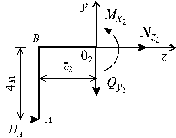 Рис. 5.19
Рис. 5.19
|
Сделав сечение в пределах этого участка, составим уравнения равновесия для левой части:
Sy = 0, 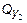 = 0;
= 0;
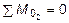 , -
, - 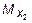 - HA×4 = 0,
- HA×4 = 0,
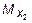 = - HA×4 = -4×4 = -16 кН×м;
= - HA×4 = -4×4 = -16 кН×м;
Sz = 0, HA + 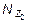 = 0,
= 0, 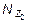 = - HA = -4 кH.
= - HA = -4 кH.
Знак “минус” перед 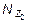 говорит о том, что элемент ВС сжат, а не растянут. Из полученных уравнений видно, что на участке II поперечная сила равна нулю, а изгибающий момент и нормальная сила постоянны.
говорит о том, что элемент ВС сжат, а не растянут. Из полученных уравнений видно, что на участке II поперечная сила равна нулю, а изгибающий момент и нормальная сила постоянны.
Участок III (0 £ z3 £ 4 м) (рис. 5.20). Приняв начало координат в сечении D и сделав разрез в пределах этого участка, рассмотрим равновесие правой отсеченной части длиной z3 . Составив уравнения равновесия Sy = 0; 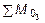 = 0 и Sz = 0 и решив их, получим:
= 0 и Sz = 0 и решив их, получим:
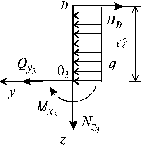 Рис. 5.20
Рис. 5.20
|
Sy = 0, 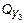 - HD + q×z3 = 0,
- HD + q×z3 = 0,
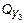 = HD - q×z3 - уравнение прямой.
= HD - q×z3 - уравнение прямой.
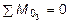 ,
, 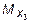 + HD ×z3 -
+ HD ×z3 - 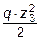 ,
,
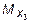 = -HD ×z3 +
= -HD ×z3 + 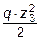 - уравнение квадратной параболы;
- уравнение квадратной параболы;
Sz = 0, Nz = 0.
Ординаты эпюр найдем из полученных выражений, подставив в них значения z3 , соответствующие граничным сечениям участка:
при z3 = 0 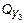 = 8 кН,
= 8 кН, 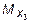 = 0,
= 0, 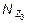 = 0;
= 0;
при z3 = 4 м 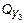 = 8 - 2×4 =0,
= 8 - 2×4 =0, 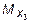 = -8×4 +
= -8×4 + 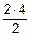 = -16 кН×м,
= -16 кН×м, 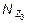 = 0.
= 0.
Для уточнения очертания квадратной параболы определим величину 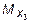 при z3 = 2 м:
при z3 = 2 м:
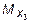
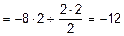 кН×м.
кН×м.
Построение эпюр Qy , Mx и Nz для бруса с ломанной осью (рамы)
Отложив в масштабе перпендикулярно к оси каждого элемента рамы полученные значения Qy , Mx , Nz в граничных и промежуточных сечениях участка и соединяя концы ординат линиями, соответствующими выражениям Qy , Mx и Nz , строим их эпюры (рис. 5.17, в, г, д).
Правильность построения эпюр внутренних усилий подтверждается на основе статической проверки, заключающейся в том, что условия равновесия рамы (Sx º 0; Sy º 0; SM º 0;), как в целом, так и любой ее отсеченной части, под воздействием внешних нагрузок и усилий, возникающих в проведенных сечениях, соблюдаются тождественно.
Дата добавления: 2017-03-12; просмотров: 1609;











