Пример расчета (задача № 2)
Абсолютно жесткий брус АЕ (рис. 2.12, а), имеющий одну шарнирно неподвижную опору С и прикрепленный в точках В, Д и Е тремя тягами из упруго-пластического материала, нагружен переменной по величине силой Р. Площадь поперечного сечения тяг F1, F2, F3, модуль упругости и предел текучести материала тяг Е = 2×105 МПа, sТ = 240 МПа. Допускаемое напряжение [s]= 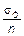 , где коэффициент запаса прочности n принят равным 1,5.
, где коэффициент запаса прочности n принят равным 1,5.
Требуется:
1. Найти усилия в тягах, реакцию опоры С и угловое смещение (поворот бруса вокруг точки С) как функции от величины силы Р;
2. Определить в процессе увеличения нагрузки Р такую ее величину, при которой напряжение в одной из тяг достигает предела текучести;
3. Определить в процессе увеличения нагрузки Р ее предельную величину, при которой напряжения в трех тягах достигнут предела текучести, реакцию опоры С и соответствующий этому предельному состоянию угол;
4. Найти величины несущей способности конструкции из расчетов по методам допускаемых напряжений и разрушающих нагрузок при одном и том же коэффициенте запаса прочности. Сопоставить результаты и сделать вывод.
Дано: F1 = 2×10-4 м2; F2 = 1×10-4 м2; F3 = 2×10-4 м2; a = 2 м; b = 1 м; c = 1 м; d = 2 м; l1 = 1 м; l2 = 1 м; l3 = 1,2 м.
Решение
1. Найти усилия в тягах, реакции в опоре С и угловое смещение (поворот бруса вокруг т. С), как функции от величины силы Р. Для определения величин усилий в тягах в зависимости от Р применим метод сечений. Сделав сечение по всем тягам и приложив в местах сечений усилия N1, N2 и N3, возникающие в тягах, рассмотрим равновесие оставшейся части, нагруженной продольными усилиями в тягах N1, N2 и N3 реакциями опоры С (RC и HC) и силой Р (рис. 2.12, б). Составив уравнения равновесия статики для оставшейся части, получим:
1) Sz = 0, НC = 0; (2.29)
2) Sy = 0, -Р + N1 + RC - N2 - N3 = 0; (2.30)
3) SMC = 0, -Р×3 + N1×1 + N2×1 + N3×3 = 0. (2.31)

Рис. 2.12
Из уравнений равновесия видно, что система дважды статически неопределима, т.к. два уравнения равновесия (2.30) и (2.31) содержат в своем составе четыре неизвестных. Поэтому для решения задачи необходимо составить два дополнительных уравнения совместности деформаций, раскрывающих статическую неопределимость системы.
Для составления дополнительных уравнений рассмотрим деформированное состояние системы (рис. 2.12, в), имея в виду, что брус абсолютно жесткий и поэтому после деформации тяг останется прямолинейным.
Эти дополнительные уравнения совместности деформаций получим из подобия треугольников ВСВ1~DCD1 и BCB1~ECE1:
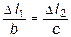 и
и 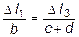 .
.
Решая эти уравнения, получим:
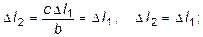 (2.32)
(2.32)
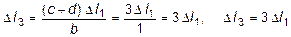 . (2.33)
. (2.33)
Выразив деформации тяг по формуле определения абсолютного удлинения:
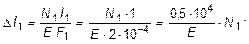
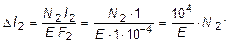
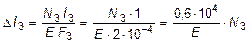
и подставив эти значения в уравнения (2.32) и (2.33), получим:
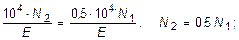 (2.34)
(2.34)
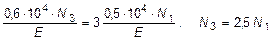 . (2.35)
. (2.35)
Подставив найденные значения N2 и N3 в уравнение (2.31) определяем величину N1 :
-P×3 + N1×1 + 0,5×N1×1 + 2,5×N1×3 = 0; N1=0,3333P.
Зная N1, из уравнений (2.34) и (2.35), находим N2 и N3:
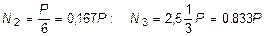 .
.
Опорную реакцию RC определяем из уравнения (2.30), подставив найденные значения N1, N2 и N3:
-P + 0,333P + RC - 0,167P - 0,833P = 0; RC = 1,667P.
После определения величин усилий в тягах N1, N2, N3 и реакции RC необходимо проверить правильность их вычисления. Для этого составим уравнение равновесия статики SМA = 0:
-N1×a - RC (a + b) + N2 (a + b + c) + N3 (a + b + c + d) = 0;
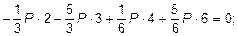
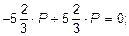 0 = 0.
0 = 0.
Следовательно, N1, N2, N3 и RC определены правильно.
Угловое смещение бруса (угол j), ввиду его малости, находим как тангенс угла наклона бруса АЕ :
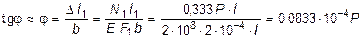 [рад].
[рад].
2. Определить в процессе увеличения нагрузки Р такую ее величину, при которой напряжение в одной из тяг достигнет предела текучести. Для вычисления величины Р, при которой напряжение в одной из тяг достигнет предела текучести sT , определим нормальные напряжения, возникающие в тягах, учитывая то, что тяги работают на растяжение:
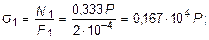
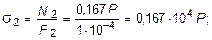
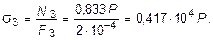
Полученные величины напряжений показывают, что в тяге 3 напряжение достигнет предела текучести раньше, чем в тягах 1 и 2, так как s3 > s1 и s3 > s2. Поэтому, приравняв напряжение s3 пределу текучести sT , определим величину Р, при которой нормальное напряжение в тяге 3 достигнет предела текучести sT :
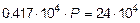 кПа,
кПа,
откуда
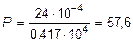 кН.
кН.
3. Определить в процессе увеличения нагрузки Р ее предельную величину, при которой напряжения в трех тягах достигнут предела текучести, реакцию опоры С и соответствующий этому предельному состоянию угол.При исчерпании несущей способности всех тяг напряжения в них достигнут предела текучести sT . В этом случае предельные усилия, которые возникнут в тягах, будут равны:
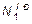 = F1×sT = 2×10-4×24×104 = 48 кH;
= F1×sT = 2×10-4×24×104 = 48 кH;
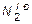 = F2 sT = 1×10-4×24×104 = 24 кH;
= F2 sT = 1×10-4×24×104 = 24 кH;
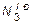 = F3×sT = 2×10-4×24×104 = 48 кH.
= F3×sT = 2×10-4×24×104 = 48 кH.
Предельную величину внешней нагрузки, соответствующую исчерпанию несущей способности, найдем из уравнения (2.31), подставив в него предельные значения 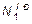 ,
, 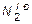 ,
, 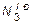 :
:
-PПР ×3 + 48×1 + 24×1 + 48×3 = 0; PПР = 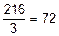 кН.
кН.
Предельную величину реакции 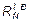 определяем из уравнения (2.30):
определяем из уравнения (2.30):
-72 + 48 + 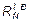 - 24 - 48 = 0;
- 24 - 48 = 0; 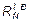 = 96 кН.
= 96 кН.
При определении наименьшего угла поворота бруса, соответствующего предельному состоянию системы, необходимо знать, в какой из тяг текучесть наступит позже.
Полученные величины напряжений (см. п. 2) показывают, что в тягах 1 и 2 напряжения достигнут предела текучести одновременно, но позже, чем в тяге 3. Поэтому предельный угол поворота бруса определяем для момента перехода материала тяг 1 и 2 в пластическое состояние:
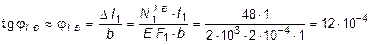 рад,
рад,
или
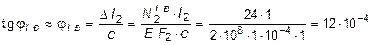 рад.
рад.
4. Найти несущую способность из расчетов по методам допускаемых напряжений и разрушающих нагрузок при одном и том же коэффициенте запаса прочности. Сопоставить результаты и сделать вывод. Из предыдущих расчетов (см. п. 2) видно, что текучесть материала раньше появится в тяге 3, т.к. s3 > s1 и s3 > > s2. Поэтому для определения величины грузоподъемности из расчета по методу допускаемых напряжений приравниваем напряжение в этой тяге s3 = 0,417×104 Р к допускаемому напряжению:
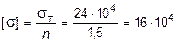 кПа, 0,417×104 [P] = 16×104 кПа,
кПа, 0,417×104 [P] = 16×104 кПа,
[P] = 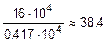 кH.
кH.
Несущая способность конструкции из расчета по методу разрушающих нагрузок получим путем деления ранее полученного значения PПР = 72 кН на коэффициент запаса n1 = 1,5:
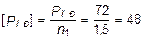 кH.
кH.
Сравнивая полученные величины, видим, что несущая способность из расчета по методу разрушающих нагрузок больше несущей способности из расчета по методу допускаемых напряжений на 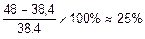 , что подтверждает известное положение о том, что метод допускаемых напряжений, в отличии от метода разрушающих нагрузок, не позволяет определить полную несущую способность системы. Это объясняется тем, что для статически неопределимых систем, переход одного элемента в пластическую стадию работы, как правило, не означает наступления предельного состояния. Переход системы в предельное состояние отождествляется с превращением ее из неизменяемой в геометрически изменяемую систему. Известно, что в статически неопределимой системе разрушение “лишних связей” не превращает ее в геометрически изменяемую. Так как реальные сооружения чаще всего представляют собой многократно статически неопределимые системы, материал которых обладает свойством пластичности, поэтому метод предельного равновесия имеет важное значение для раскрытия истинных резервов их несущей способности.
, что подтверждает известное положение о том, что метод допускаемых напряжений, в отличии от метода разрушающих нагрузок, не позволяет определить полную несущую способность системы. Это объясняется тем, что для статически неопределимых систем, переход одного элемента в пластическую стадию работы, как правило, не означает наступления предельного состояния. Переход системы в предельное состояние отождествляется с превращением ее из неизменяемой в геометрически изменяемую систему. Известно, что в статически неопределимой системе разрушение “лишних связей” не превращает ее в геометрически изменяемую. Так как реальные сооружения чаще всего представляют собой многократно статически неопределимые системы, материал которых обладает свойством пластичности, поэтому метод предельного равновесия имеет важное значение для раскрытия истинных резервов их несущей способности.
Дата добавления: 2017-03-12; просмотров: 1609;











