Потенциальная энергия деформации
Внешние силы, приложенные к упругому телу и вызывающие изменение геометрии тела, совершают работу А на соответствующих перемещениях. Одновременно с этим в упругом теле накапливается потенциальная энергия его деформирования U. При действии динамических внешних нагрузок часть работы внешних сил превращается в кинетическую энергию движения частиц тела К. Приняв энергетическое состояние системы до момента действия данных сил равным нулю, и в условиях отсутствия рассеивания энергии, уравнение баланса энергии можно записать в следующем виде:
А = U + K. (2.8)
При действии статических нагрузок К = 0, следовательно,
А = U. (2.9)
Это означает, что при статическом нагружении работа внешних сил полностью преобразуется в потенциальную энергию деформации. При разгрузке тела производится работа за счет потенциальной энергии деформации, накопленной телом. Таким образом, упругое тело является аккумулятором энергии. Это свойство упругого тела широко используется в технике, например, в заводных пружинах часовых механизмов, в амортизирующих рессорах и др. В случае простого растяжения (сжатия) для вывода необходимых расчетных зависимостей потенциальной энергии деформации рассмотрим решение следующей задачи.
На рис. 2.4, а изображен растягиваемый силой Р стержень, удлинение которого соответствует отрезку Dl, ниже показан график изменения величины удлинения стержня Dl в зависимости от силы Р (рис. 2.4, б). В соответствии с законом Гука этот график носит линейный характер.

|
Пусть некоторому значению силы Р соответствует удлинение стержня Dl. Дадим некоторое приращение силе DР - соответствующее приращение удлинения составит d (Dl ). Тогда элементарная работа на этом приращении удлинения составит:
dA = (P + d P)×d (D l ) = P×d (D l ) + d P × d (D l ) , (2.10)
вторым слагаемым, в силу его малости, можно пренебречь, и тогда
dA = P×d (D l ). (2.11)
Полная работа равна сумме элементарных работ, тогда, при линейной зависимости “нагрузка - перемещение”, работа внешней силы Р на перемещении Dl будет равна площади треугольника ОСВ (рис. 2.4), т.е.
А = 0,5 Р×Dl . (2.12)
В свою очередь, когда напряжения s и деформации e распределены по объему тела V равномерно (как в рассматриваемом случае) потенциальную энергию деформирования стержня можно записать в виде:
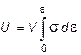 . (2.13)
. (2.13)
Поскольку, в данном случае имеем, что V = F l, P = s F иs = Е e,то
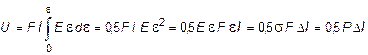 , (2.14)
, (2.14)
т.е. подтверждена справедливость (2.9).
С учетом (2.5) для однородного стержня с постоянным поперечным сечением и при Р = const из (2.14) получим:
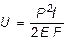 . (2.15)
. (2.15)
2.5. Статически определимые и статически
неопределимые системы
Если при рассмотрении заданной системы, находящейся в равновесном состоянии от действия заданных внешних нагрузок, все реакции в связях закрепления, а также внутренние усилия в ее элементах, можно определить только по методу сечений, без использования дополнительных условий, то такая система называется статически определимой.
Сопоставление предела прочности хрупких материалов при растяжении 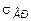 с пределом прочности при сжатии
с пределом прочности при сжатии 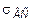 показывают, что эти материалы обладают, как правило, более высокими прочностными показателями при сжатии, нежели при растяжении. Величина отношения
показывают, что эти материалы обладают, как правило, более высокими прочностными показателями при сжатии, нежели при растяжении. Величина отношения 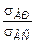 для чугуна составляет 0.2 ¸0.4, для керамических материалов 0.1¸0.2. Для пластичных материалов установлено, что
для чугуна составляет 0.2 ¸0.4, для керамических материалов 0.1¸0.2. Для пластичных материалов установлено, что 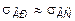 .
.
Большое влияние на проявление свойств материалов оказывает скорость нагружения и температурное воздействие. При высокоскоростном нагружении более резко проявляются свойства хрупкости, а при медленном нагружении - свойства пластичности. Например, хрупкое стекло способно при длительном воздействии нагрузки в условиях нормальной температуры (+20оС) проявляет пластические свойства. Пластичные же материалы, такие, как малоуглеродистая сталь, при воздействии ударных нагрузок проявляет хрупкие свойства. В зависимости от указанных обстоятельств механические свойства материалов проявляются по-разному. Обобщенный анализ свойств материалов с учетом температуры и времени оказывается очень сложным. Функциональная зависимость между четырьмя параметрами s, e, температурой to и временем t, т.е. 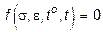 не является адекватной и содержит в сложной форме дифференциальные и интегральные соотношения, входящих в нее величин.
не является адекватной и содержит в сложной форме дифференциальные и интегральные соотношения, входящих в нее величин.
Так как в обобщенной форме, точное аналитическое выражение функции f получить невозможно, то влияние температуры и фактора времени рассматривается в настоящее время применительно только к частным классам задач. Деление на классы производится как по характеру действия внешних сил так и по типу материалов, а также в зависимости от скорости нагружения.
Наиболее, изучаемыми в механике материалов, являются процессы происходящие при действии медленно изменяющихся (статических) нагрузок.
Скорость изменения этих нагрузок во времени настолько мала, что кинетическая энергия деформируемого тела, составляет незначительную долю от работы внешних сил. Поэтому работа внешних сил превращается только в упругую энергию и в необратимую тепловую энергию, связанную с пластическими деформациями тела.
При статических испытаниях материалов 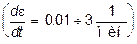 в различных температурных режимах определяется зависимость механических характеристик материалов от температуры. Эта зависимость характеризует изменения внутрикристаллических и межкристаллических связей, а в некоторых случаях и структурными изменениями материалов. В общем случае с ростом температуры, прочностные характеристики материалов существенно падают. При этом, чем выше температура, тем труднее определить механические характеристики материалов. Происходит это не только потому, что возрастают сложности в технике эксперимента, но также вследствие того, что сама характеристика становится менее определенной.
в различных температурных режимах определяется зависимость механических характеристик материалов от температуры. Эта зависимость характеризует изменения внутрикристаллических и межкристаллических связей, а в некоторых случаях и структурными изменениями материалов. В общем случае с ростом температуры, прочностные характеристики материалов существенно падают. При этом, чем выше температура, тем труднее определить механические характеристики материалов. Происходит это не только потому, что возрастают сложности в технике эксперимента, но также вследствие того, что сама характеристика становится менее определенной.
При статическом нагружении, начиная с некоторых значений температур, фактор времени становится очень существенным. Для разных материалов это явление происходит при совершенно различных температурных режимах. Влияние фактора времени обнаруживается и при нормальных температурах. Для металлов его влияние, из-за незначительности, можно пренебречь. А для органических материалов даже при низких температурах время нагружения имеет существенное значения.
В заключение отметим наиболее важные свойства материалов которые обнаруживаются при их испытаниях. Эти свойства имеют фундаментальное значение при построении физических уравнений механики твердого деформируемого тела.
Упругость - это способность твердого деформируемого тела восстанавливать свою форму и объем после прекращения действия внешних нагрузок.
Пластичность - это свойство твердого деформируемого тела до разрушения необратимо изменять свою форму и объем от действия внешних сил.
Вязкость - это свойство оказывать сопротивление за счет трения происходящего при перемещении элементарных частиц тела относительно друг друга в процессе деформирования. Отметим, что при этом, как показывают результаты экспериментов, сила сопротивления, возникающая за счет внутреннего трения материалов, прямым образом зависит от величины скорости перемещения элементарных частиц относительно друг друга.
Упругость, пластичность и вязкость являются главными физическими свойствами твердого деформируемого тела.
Ползучесть - это явление характеризующееся изменения во времени величин деформаций и напряжений в теле при действии статических нагрузок.
Выносливость - при действии периодически изменяющихся по времени нагрузок, это явление, которое характеризуется чувствительностью и изменениями прочностных свойств материалов в зависимости от числа циклов нагружения.
В реальной практике встречаются такие конструкции при расчете которых одних лишь уравнений равновесия оказывается недостаточно, в связи с чем требуется формулирование дополнительных уравнений, связанных с условиями деформирования конструкции.
Системы, в которых количество наложенных связей больше, нежели число независимых уравнений равновесия, называются статически неопределимыми.
По сравнению со статически определимыми системами, в статически неопределимых системах имеются дополнительные связи, которые называются лишними.
Термин “лишние связи” является условным. Эти связи являются лишними с точки зрения расчетных предпосылок. В действительности эти связи создают дополнительные резервы для конструкций, как в плане обеспечения её жесткости, так и прочности.
На рис. 2.5, а изображен кронштейн, состоящий из двух стержней, шарнирно скрепленных между собой. В связи с тем, что на конструкцию действует лишь вертикальное усилие Р, а система является плоской (т.е. все элементы конструкции и вектор внешних сил лежат в одной плоскости), получается, что усилия в стержнях легко определяются из условий равновесия узла А, т.е.
åx = 0, åy = 0. (2.16)
Раскрывая эти уравнения, получаем замкнутую систему линейных уравнений относительно неизвестных усилий N1 и N2 в которой количество уравнений равно количеству неизвестных:
-N1 - N2 sin a = 0; -N2 cos a - Р = 0.

Рис. 2.5
Если конструкцию кронштейна усложнить, добавив еще один стержень (рис. 2.5, б), то усилия в стержнях N1, N2 и N3 прежним способом определить уже не удастся, т.к. при тех же двух уравнениях равновесия (2.16) имеются уже три неизвестных усилия в стержнях. В таких случаях говорят, что система один раз статически неопределима. Разность между числом неизвестных усилий и количеством независимых (значащих) уравнений равновесия, связывающих эти усилия, называется степенью статической неопределимости рассматриваемой системы.
В общем случае под n-раз статически неопределимой системой понимается система, в которой число неизвестных внешних опорных реакций и внутренних усилий превышает число независимых и значащих уравнений равновесия на n единиц.
2.6. Напряженное и деформированное состояние
при растяжении и сжатии
Рассмотрим более подробно особенности напряженного состояния, возникающего в однородном растянутом стержне. Определим напряжения, возникающие на некоторой наклонной площадке, составляющей угол a с плоскостью нормального сечения (рис. 2.6, а).
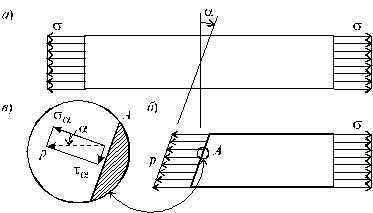
Рис. 2.6
Из условия åz = 0, записанного для отсеченной части стержня (рис. 2.6, б), получим:
р Fa = s F, (2.17)
где F - площадь поперечного сечения стержня, Fa = F/cos a - площадь наклонного сечения. Из (2.17) легко установить:
р = s сos a. (2.18)
Раскладывая напряжение р по нормали и касательной к наклонной площадке (рис. 2.6, в), с учетом (2.18) получим:
sa = p cos a = s cos2 a; ta = p sin a = 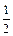 s sin 2 a . (2.19)
s sin 2 a . (2.19)
Полученные выражения показывают, что для одной и той же точки тела величины напряжений, возникающих в сечениях, проходящих через эту точку, зависят от ориентации этой площадки, т.е. от угла a. При a = 0 из (2.19) следует, что sa = s, ta = 0. При a = 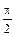 , т.е. на продольных площадках, sa = ta = 0. Это означает, что продольные слои растянутого стержня не взаимодействуют друг с другом. Касательные напряжения ta принимают наибольшие значения при a =
, т.е. на продольных площадках, sa = ta = 0. Это означает, что продольные слои растянутого стержня не взаимодействуют друг с другом. Касательные напряжения ta принимают наибольшие значения при a = 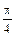 , и их величина составляет tmax=
, и их величина составляет tmax= 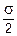 . Важно отметить, как это следует из (2.19), что
. Важно отметить, как это следует из (2.19), что 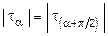 . Следовательно, в любой точке тела на двух взаимно перпендикулярных площадках касательные напряжения равны между собой по абсолютной величине. Это условие является общей закономерностью любого напряженного состояния и носит название закона парности касательных напряжений.
. Следовательно, в любой точке тела на двух взаимно перпендикулярных площадках касательные напряжения равны между собой по абсолютной величине. Это условие является общей закономерностью любого напряженного состояния и носит название закона парности касательных напряжений.
Теперь перейдем к анализу деформаций в растянутом стержне. Наблюдения показывают, что его удлинение в продольном направлении сопровождается пропорциональным уменьшением поперечных размеров стержня (рис. 2.7).
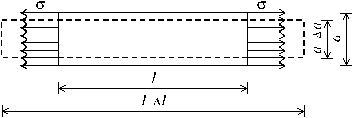
Рис. 2.7
Если обозначить:
 eпрод =
eпрод = 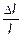 ; eпопер = -
; eпопер = - 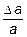 , m = -
, m = - 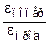 ,
,
то, как показывают эксперименты, m = const для данного материала и является безразмерным коэффициентом Пуассона. Величина m является важной характеристикой материала и определяется экспериментально. Для реальных материалов m принимает значения 0,1 ¸ 0,45.
При растяжении стержня возникают не только линейные, но и угловые деформации.
Рассмотрим прямой угол АВС (рис. 2.8, а), образованный отрезками АВ и АС, в недеформированном состоянии.
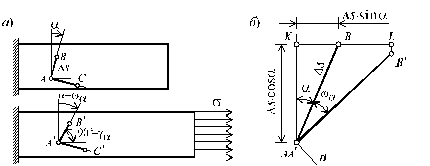
Рис. 2.8
При растяжении стержня точки А, В и С займут положение А ¢, B ¢, C ¢ соответственно. Величина
ga = ÐВАС - ÐА ¢B ¢C ¢
называется угловой деформацией или угловым сдвигом в точке А.
Совместим точки А и А ¢ и рассмотрим взаимное расположение отрезков АВ и А ¢B ¢(рис. 2.8, б). На этом рисунке отметим вспомогательные точки K и L и прямую n, перпендикулярную отрезку А ¢B ¢. Из рис. 2.8, б имеем:
eпрод = 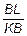 ; eпопер =
; eпопер = 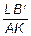 ,
,
откуда с учетом eпрод = 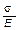 получим:
получим:
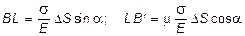 . (2.20)
. (2.20)
Для определения wa спроектируем ломаную ВLB ¢А ¢на ось n DS×sin wa = BL cos (a + wa) + LB ¢sin(a + wa), откуда, учитывая малость угла wa , т.е. sin wa » wa , cos wa » 1, получим:
wa = 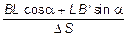 . (2.21)
. (2.21)
В результате совместного рассмотрения (2.20) и (2.21) получим:
wa = 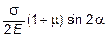 .
.
Откуда
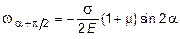 .
.
Следовательно,
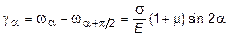 . (2.22)
. (2.22)
Сопоставляя выражение ga с выражением ta из (2.17) окончательно получим закон Гука для сдвига:
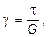 (2.23)
(2.23)
где величина 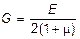 называется модулем сдвига или модулем упругости материала второго рода.
называется модулем сдвига или модулем упругости материала второго рода.
2.7. Основные механические характеристики
материалов
Для количественной оценки основных свойств материалов, как
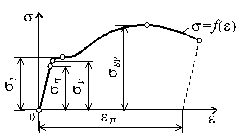 Рис. 2.9
Рис. 2.9
|
правило, экспериментально определяют диаграмму растяжения в координатах s и e (рис. 2.9), На диаграмме отмечены характерные точки. Дадим их определение.
Наибольшее напряжение, до которого материал следует закону Гука, называется пределом пропорциональности sП . В пределах закона Гука тангенс угла наклона прямой s = f (e) к оси e определяется величиной Е.
Упругие свойства материала сохраняются до напряжения sУ , называемого пределом упругости. Под пределом упругости sУ понимается такое наибольшее напряжение, до которого материал не получает остаточных деформаций, т.е. после полной разгрузки последняя точка диаграммы совпадает с начальной точкой 0.
Величина sТ называется пределом текучести материала. Под пределом текучести понимается то напряжение, при котором происходит рост деформаций без заметного увеличения нагрузки. Если необходимо различать предел текучести при растяжении и сжатии sТ соответственно заменяется на sТР и sТС . При напряжениях больших sТ в теле конструкции развиваются пластические деформации eП , которые не исчезают при снятии нагрузки.
Отношение максимальной силы, которую способен выдержать образец, к его начальной площади поперечного сечения носит название предела прочности, или временного сопротивления, и обозначается через, sВР (при сжатии sВС ).
В табл. 2 приводятся значения указанных характеристик (в кН/м2) наиболее распространенных конструкционных материалов.
Таблица 2
| Материал | sТР | sТС | sВР | sВС | Е×10-8 |
| Сталь | - | ||||
| Чугун | 0.7 | ||||
| Медь | - | 1.1 | |||
| Алюминий | - | 0.75 |
При выполнении практических расчетов реальную диаграмму (рис. 2.9) упрощают, и с этой целью применяются различные аппроксимирующие диаграммы. Для решения задач с учетом упруго-пластических свойств материалов конструкций чаще всего применяется диаграмма Прандтля. По этой диаграмме напряжение изменяется от нуля до предела текучести по закону Гука s = Е e, а далее при росте e, s = sТ (рис. 2.10).
Способность материалов получать остаточные деформации носит название пластичности. На рис. 2.9 была представлена характерная диаграмма для пластических материалов.

Рис. 2.10 Рис. 2.11
Противоположным свойству пластичности является свойство хрупкости, т.е. способность материала разрушаться без образования заметных остаточных деформаций. Материал, обладающий этим свойством, называется хрупким. К хрупким материалам относятся чугун, высокоуглеродистая сталь, стекло, кирпич, бетон, природные камни. Характерная диаграмма деформации хрупких материалов изображена на рис. 2.11.
Дата добавления: 2017-03-12; просмотров: 3585;











