Внутренние силы и напряжения
Под растяжением (сжатием) понимают такой вид нагружения, при котором в поперечных сечениях стержня возникают только нормальные силы, а прочие силовые факторы равны нулю.
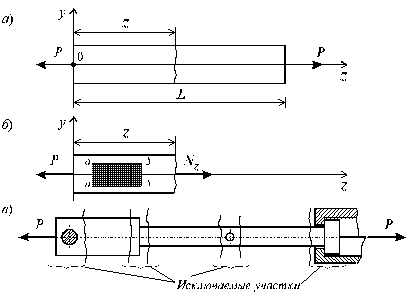
Рассмотрим однородный прямолинейный стержень длиной l и площадью поперечного сечения F, на двух концах которого приложены две равные по величине и противоположно направленные центральные продольные силы Р (рис. 2.1, а). Поместим начало плоской системы координат yz в центре тяжести левого сечения, а ось z направим вдоль продольной оси стержня.
Для определения величин внутренних усилий воспользуемся методом сечений. Задавая некоторое сечение на расстояние z (0 £ z £ l) от начала системы координат и рассматривая равновесие левой относительно заданного сечения части стержня (рис. 2.1, б), приходим к следующему уравнению:
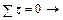 P + Nz = 0,
P + Nz = 0,
откуда следует, что
Nz = P = const.
Примем для Nz следующее правило знаков. Если Nz направлена от сечения, т.е. вызывает положительную деформацию (растяжение), то она считается положительной. В обратном случае - отрицательной.
|
Рис. 2.1
Нормальная сила Nz приложена в центре тяжести сечения, является равнодействующей внутренних сил в сечении и, в соответствии с этим, определяется следующим образом:
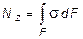 .
.
Но из этой формулы нельзя найти закон распределения нормальных s напряжений в поперечных сечениях стержня. Для этого обратимся к анализу характера его деформирования.
Если на боковую поверхность этого стержня нанести прямоугольную сетку (рис. 2.1, б), то после нагружения поперечные линии а-а, b-b и т.д. переместятся параллельно самим себе, откуда следует, что все поверхностные продольные волокна удлинятся одинаково. Если предположить также, что и внутренние волокна работают таким же образом, то можно сделать вывод о том, что поперечные сечения в центрально растянутом стержне смещаются параллельно начальным положениям, что соответствует гипотезе плоских сечений, введенной швейцарским ученым Д. Бернулли, гласящей, что плоские сечения до деформации остаются плоскими и после деформации.
Значит, все продольные волокна стержня находятся в одинаковых условиях, а следовательно, нормальные напряжения во всех точках поперечного сечения должны быть также одинаковы и равны
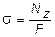 ,
,
где F - площадь поперечного сечения стержня.
Высказанное предположение о равномерном распределении внутренних сил в поперечном сечении справедливо для участков, достаточно удаленных от мест: резкого изменения площади поперечного сечения (рис. 2.1, в); скачкообразного изменения внешних нагрузок; скачкообразного изменения физико-механических характеристик конструкций. Основанием для такого утверждения служит принцип Сен-Венана, справедливый для любого типа напряженного состояния и формулируемый следующим образом: особенности приложения внешних нагрузок проявляются, как правило, на расстояниях, не превышающих характерных размеров поперечного сечения стержня.
Дата добавления: 2017-03-12; просмотров: 1834;











