Расчет червячной передачи по напряжениям изгиба

Для прямозубых зубчатых колёс условие прочности по изгибным напряжениям

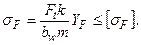Для червячного колеса (рис. 10.6)

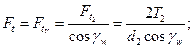
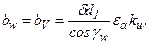
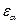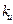где и - учитывают наличие перекрытия и реальную длину линии контакта;

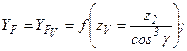
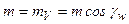Тогда условие прочности для червячного колеса запишется

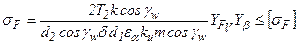где Y_b=cos²g_w – коэффициент, учитывающий отличия в работе биэквивалентного прямозубого колеса и реального червячного колеса, или

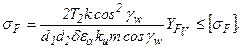
Для средних приведенных значений d=50⁰;e_a=1,6; k_u= 0,75 получим

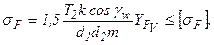
Для проектировочного расчета модуль определяют по зависимости m=d₂/z₂.

Здесь d₂ принимают из проектировочного расчета на контактную выносливость, а z₂= z₁U, где z₁ – число заходов.

Тепловой расчет червячного редуктора

Механическая энергия, затрачиваемая на преодоление сил трения в червячном редукторе, превращается в тепло. Повышение температуры приводит к снижению вязкости в смазке и её защитных свойств, что приводит к вероятности задиров. Условие теплового расчета t_m £ [t_m], где [t_m] = 80…95 ⁰C, для авиационных масел [t_m] =110 ⁰C – допускаемая температура масла.

Мощность теплового потока выделяемого в результате работы сил трения

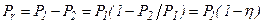Мощность, отводимая в результате охлаждения определяется по зависимости

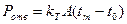Здесь k_T=12…19 Вт/м²·С⁰– коэффициент теплоотдачи от поверхности корпуса редуктора; А – поверхность охлаждения, [м²]; (t_m-t₀) – разность температур масла и окружающего воздуха [⁰C] , где t₀=20 ⁰С.

Таким образом, в связи с наличием трения тепло подводится, а из-за теплоотдачи отводится. С течением времени установится постоянная температура вследствие теплового баланса, т.к. P_r=P_отв_.Следовательно можно записать

1000P₁(1-h)=k_TA(t_m-t₀).

Из последнего уравнения находят

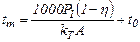Если оказалось, что t_m_> [t_m], то используют следующие мероприятия:

Снижают потери на трение;
Увеличивают поверхность охлаждения за счет оребрения;
Применяют искусственное охлаждение – обдув, водяное охлаждение масляной ванны, циркуляционная смазка. За счет этого k_T можно увеличить в 10 и более раз.

Лекция №11

Ременные передачи

Элементы геометрии ременной передачи

Ременная передача состоит из ведущего и ведомого шкивов, соединенных ремнем. Ремни бывают плоские, клиновидные и круглые (рис. 11.1). Нагрузка передается силами трения между шкивом и ремнем. При геометрическом расчете обычно известны d₁ и d₂ – диаметры шкивов и межосевое расстояние а. Определяется угол охвата ремнем малого шкива α через угол между ветвями ремня β и длину ремня l. Вследствие вытяжки и провисания ремня, величины α и l не являются строгими и определяются приближенно. Из рис.11.1 видно, что α=180⁰-β. Проведем из О₁ линии параллельно ремню. Они отсекут на диаметре d₂ окружность d₂ - d₁. 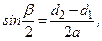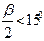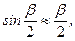Из ∆О₁О₂В видно, что так как , то т.е.

; .

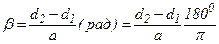Длина ремня определяется как сумма прямолинейных участков и дуг охвата

Используя ряд Макларена для 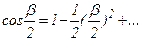, можно записать

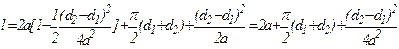
Скольжение в ременной передаче

Исследования Н.Е. Жуковского показали, что в ременных передачах следует различать два вида скольжения ремня по шкиву - упругое скольжение и буксование. Природа упругого скольжения может быть установлена из следующего опыта. Пусть ремень расположен на заторможенном шкиве (рис. 11.2). В начале опыта к концам ремня подвешены равные грузы F. Под действием грузов между ремнем и шкивом возникает сила трения, затем левая часть ветви догружается грузом F₁. Если сила F₁ будет больше сил трения между ремнем и шкивом, то равновесие нарушится и ремень соскользнет со шкива. Под дополнительным грузом ремень растянется на дуге l₁. Длина дуги зависит от F₁ и силы трения на этом участке. Дополнительное упругое удлинение ремня будет сопровождаться его скольжением по шкиву. Это скольжение принято называть упругим, а дугу l₁ – дугой упругого скольжения. Дуга l₂ называется дугой покоя.

При увеличении силы F₁ до значения, равного запасу сил трения (l₂=0) равновесие нарушится и начнется буксование.

В реальной передаче (рис 11.3) роль грузов F выполняет сила натяжения ведомой ветви F₂, а роль дополнительного груза F₁ – окружная сила F_t. Здесь F₀ – предварительное натяжение ремня. Разность натяжения ведомой и ведущей ветви, создаваемая нагрузкой, вызывает упругое скольжение. При этом дуги упругого скольжения расположены по разные стороны сбегающей ветви.

Передаточное число ременной передачи

Выделим некоторый участок ремня длиной l в ненагруженной передаче, а затем дадим нагрузку. При прохождении ведущей ветви отмеченный участок удлинится l+∆, а ведомой сократится l-∆, тогда окружные скорости будут

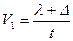и ,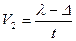

где t - время прохождения участка. Значит скорость V₂<V₁.

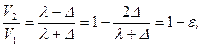
где 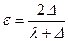- коэффициент скольжения.

Тогда V₂=V₁(1-e).

Окружные скорости

; .

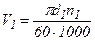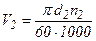Отношение 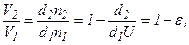тогда .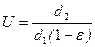

По мере роста нагрузки увеличивается ∆, а значит, возрастает разность окружных скоростей и меняется передаточное отношение. Упругое скольжение является причиной некоторого непостоянства передаточного отношения в ременной передаче. При перегрузке дуга покоя уменьшается до 0, ремень начинает скользить по всей поверхности шкива, наступает режим буксования. При этом ведомый шкив останавливается, а КПД передачи равен 0.

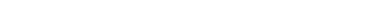Силы в ременной передаче

Рассмотрим два случая (рис. 11.4). В первом случае (рис. 11.4, а) нагрузка отсутствует (Т₁=0). Здесь F₀ – предварительное натяжение ремня. Во втором случае (Рис. 11.4, б) передача нагружена моментом Т₁>0. Здесь F₁ и F₂ – натяжение ведущей и ведомой ветвей. Окружная сила .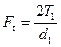

По условию равновесия шкива имеем

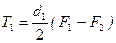или 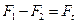(11.1).

Связь между F₀, F₁ и F₂ можно установить на основе следующих рассуждений. Геометрическая длина ремня не зависит от нагрузки и остается неизменной как в ненагруженной, так и в нагруженной передаче. Следовательно, дополнительная вытяжка ведущей ветви компенсируется сокращением ведомой. Согласно закону Гука деформация пропорциональна силе, тогда запишем

F₁=F₀+∆F, F₂=F₀- ∆F или F₁+F₂ =2F₀. (11.2).

Из совместного решения уравнений (11.1)и(11.2) получим

, .

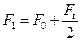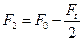Последние уравнения устанавливают изменение натяжения ведущей и ведомой ветвей в зависимости от нагрузки F_t и предварительного натяжения F₀, но не вскрывают тяговой способности передачи, которая связана с величиной сил трения между ремнем и шкивом. Эта связь установлена Л. Эйлером. Он установил зависимость между F₁ и F₂ на границе буксования, то есть определил максимально допустимую величину F_t в зависимости от F₀ при условии использования полного запаса сил трения.

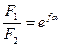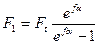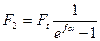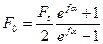; ; ; , здесь f - коэффициент трения.

При круговом движении ремня со скоростью V на каждый его элемент массой d_m, расположенный в пределах угла охвата, действуют элементарные центробежные силы dF_c(рис 11.5). Действие этих сил вызывает дополнительное натяжение F_v во всех сечениях ремня.

,

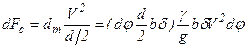где g - удельный вес ремня, g - ускорение силы тяжести, b - ширина, d - толщина ремня.

Из условия равновесия ремня получим .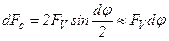

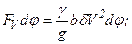
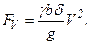
Натяжение F_v ослабляет полезное действие предварительного натяжения F₀. Оно уменьшает величину сил трения и тем самым понижает нагрузочную способность передачи.

<15 16 171819 20 21 >

Дата добавления: 2017-03-12; просмотров: 2047;