Внутренние усилия и напряжения при растяжении (сжатии)

Растяжение (сжатие) - простой вид сопротивления, при котором стержень нагружен силами, параллельными продольной оси стержня и приложенными в центр тяжести его сечения.

Рассмотрим стержень, упруго растянутый центрально приложенными сосредоточенными силами P.

Прежде чем перейти к исследованию внутренних усилий и напряжений, возникающих в растянутом стержне, рассмотрим некоторые гипотезы, связанные с характером деформирования такого стержня и имеющие в сопротивлении материалов исключительно важное значение.

Принцип Сен-Венана: в сечениях, достаточно удаленных от мест приложения сил, распределение напряжений и деформаций мало зависит от способа приложения нагрузок.

Принцип Сен-Венана дает возможность вести расчет без учета местных (локальных) деформаций, возникающих вблизи точек приложения внешних сил и отличающихся от деформаций основного объема материала, что в большинстве случаев упрощает решение задачи.

Гипотеза плоских сече-ний (гипотеза Я.Бернулли): поперечные сечения стержня плоские и перпендикулярные его оси до деформации остаются плоскими и перпендикулярными оси, и после деформации.

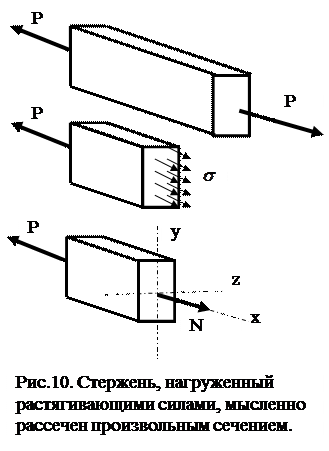
Мысленно рассекая стер-жень, определим внутренние силы в растянутом стержне:

а) стержень, нагруженный растя-гивающими силами P и находя-щийся в равновесии, рассекаем произвольным сечением;

б) отбрасываем одну из частей стержня, а ее действие на дру-гую часть компенсируем вну-тренними усилиями интенсив-ностью ;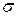

в) осевое внутреннее усилие N, возникающее в сечении стержня, определим, составляя уравнения равновесия для отсеченной части:

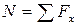. (2.1)

Проецируя внешнюю силу P, действующую на отсеченную часть стержня, на другие оси (z и y), а также составляя уравнения моментов относительно координатных осей, легко убедится, что осевое усилие N является единственным внутренним усилием, возникающим в сечении стержня (остальные тождественно равны нулю).

Таким образом, при растяжении (сжатии) из шести внутренних усилий в сечении стержня возникает только одно — продольная сила N.

Нормальные напряжения 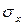, возникающие в сечении стержня, связаны с осевым усилием N следующим образом:

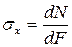, или 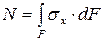. (2.2)

Учитывая, что в соответствии с гипотезой Бернулли напряжения равномерно распределены по поперечному сечению (т.е. 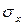=const), можно записать:

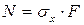. (2.3)

Таким образом, нормальные напряжения при растяжении (сжатии) определяются как

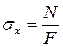. (2.4)