Математическое моделирование местности

Математические связи между исходными точками цифровых моделей описывают линейными, либо нелинейными (степенными) зависимостями. В первом случае связь между смежными точками модели описывается уравнениями плоскостей, проходящими через каждые три смежные точки модели, во втором - криволинейными поверхностями разного порядка, и, таким образом, рельеф местности задается либо множеством пересекающихся между собой плоскостей, либо поверхностей различного порядка кривизны.

Решение наиболее актуальной задачи при математическом моделировании рельефа и инженерно-геологического строения местности заключается в определении высот точек местности, а также уровней грунтовых вод и соответствующих геологических напластований в пикетных и плюсовых точках по оси запроектированных вариантов трассы и на поперечниках.

Подавляющее число регулярных и нерегулярных ЦММ предполагают при последующем математическом моделировании линейную интерполяцию высот между смежными точками модели.

Задача определения высот точек трассы, уровней грунтовых вод и поверхностей геологических напластований сводится к нахождению в каждом случае тех смежных исходных точек модели, между которыми попадает соответствующая искомая точка трассы, в нахождении коэффициентов уравнения плоскости, проходящей через эти три точки, и, наконец, в определении по полученному уравнению искомой высотызаданной точки (рис. 3.5).

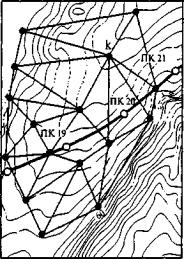
Рис. 3.5. Линейная интерполяция высот между смежными точками ЦММ

Если искомая точка трассы (например, ПК 20) попадает между смежными исходными точками ЦММ с номерами j, k и l, то уравнение искомой плоскости в общем виде может быть представлено:

H = AX + BУ + C. (3.7)

В уравнении (3.7) известны проектные координаты X и У точки трассы (например, ПК 20), высоту которой нужно определить, но не известны коэффициент А, В и С уравнения плоскости, проходящей через исходные точки j, k и l цифровой модели.

Если в уравнение (3.7) подставить известные координаты трех исходных точек цифровой модели, то получим три уравнения, в которых не известны только три коэффициента А, В и С:

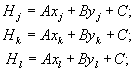(3.8)

Система уравнений (3.8) решается в матричной форме или методом «прогонки», в результате чего определяются неизвестные коэффициенты А, В и С.

Уравнение (3.7), подставив в которое проектные координаты X и У искомой точки трассы, определяет ее высоту Н.

Наиболее универсальными являются статистические ЦММ (3.6), математическая реализация которых заключается в использовании метода «плавающего квадрата» или «плавающего круга», в пределах которого строится криволинейная поверхность n-го порядка (рис. 3.6).

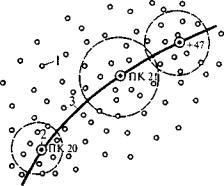
Рис. 3.6. Математическое моделирование рельефа «плавающей» криволинейной поверхностью:
1 - точки статистической ЦММ; 2 - точки трассы; 3 - трасса

Наиболее часто для математического моделирования рельефа используют уравнения поверхности 2-го порядка:

Н = АХ² + ВХУ + CУ² + DX + EУ + F, где (3.9)

Х, У - известные проектные координаты точки, высоту которой требуется определить; А, В, С, D, Е, F - коэффициенты уравнения аппроксимирующей поверхности 2-го порядка.

Основная идея «плавающей» аппроксимации заключается в том, что по трассе дороги от точки к точке перемещается круг или квадрат таким образом, что каждая точка трассы, высоту которой требуется определить, размещается в его центре (например, ПК 20 на рис. 3.6). Радиус круга или размеры стороны квадрата автоматически устанавливаются такими, чтобы в их пределы попало не менее 10 исходных точек модели. Поскольку радиус круга или размеры стороны квадрата меняются с дискретным шагом, соответственно Dr и Db, то в пределах выделяемых ими площадей может оказаться и более 10 точек модели (например, 11, 12, 13 и т.д.).

Поскольку коэффициенты А, В, С, D, Е, F в аппроксимирующем уравнении (3.9) не известны, то для каждой точки модели, попавшей в пределы круга или квадрата, записывают уравнения:

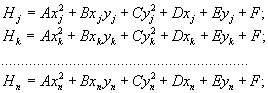где (3.10)

А, В, С, D, Е, F - неизвестные коэффициенты уравнения аппроксимируемой поверхности;

Н_j, х_j, y_j,... , Н_п, х_п, y_п - известные координаты точек модели, попавших в пределы круга или квадрата.

Поскольку число неизвестных в системе (3.10) меньше числа уравнений (которых не менее 10), то система решается методом «наименьших квадратов». Таким образом, определяют неизвестные коэффициенты аппроксимирующего уравнения (3.9), подставив в которое известные проектные координаты X и У точки трассы (например, ПК 20), определяют ее высоту Н.

Далее центр круга или квадрата перемешают в очередную точку трассы (например, на ПК 21) и процедура повторяется. При этом, если плотность исходных точек модели в районе очередной точки трассы уменьшилась, то размеры круга или квадрата автоматически возрастут, а если плотность возросла - то наоборот уменьшатся.

Для математического описания ситуационных, почвенно-грунтовых, гидрогеологических и других условий местности используют контурную индексацию объектов местности с перечнем номеров точек вдоль каждого контура (граница пашни, лес, река, ЛЭП, газопровод и т.д., например: К₃; 3; 21; 43; 24; 26. Длязамкнутых контуров (здание, сад, огород, пруд и т.д.) точки замыкания повторяются, например: С₇; 13; 15; 52; 16; 13.