Осаждение частиц при зацеплении
При осаждении частиц, размер которых соизмерим с размерами препятствия или обтекаемого тела, начинает проявляться эффект зацепления (касания). Если пренебречь инерционными эффектами и считать, что частица точно следует в соответствии с линиями тока, то частица осаждается не только в том случае, когда ее траектория пересечется с поверхностью тела, но и в случае пересечения линии тока на расстоянии от поверхности тела, равном ее радиусу. Таким образом, эффективность зацепления выше нуля и тогда, когда инерционное осаждение отсутствует.
Эффект зацепления характеризуется параметром R', который представляет собой отношение диаметров частицы dч и обтекаемого тела (препятствия)
Dпр = 2R (рис. 4.4):
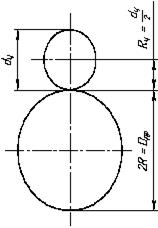
Рис. 4.4
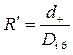 . (4.26)
. (4.26)
Например, при потенциальном («гладком») обтекании шара газовым потоком, когда величины dч и Dпр настолько малы, что можно пренебречь инерционными эффектами, эффективность зацепления составляет
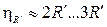 ,
,
при обтекании цилиндра
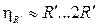 .
.
Эффективность осаждения частиц при «вязком» обтекании препятствия в значительной степени определяется режимом течения газового потока и не зависит от скорости газов. Оптимальное условие осаждения частиц в этом случае выражается отношением критерия Стокса Stk для частицы (формула (4.13) и критерия Рейнольдса ( 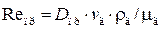 ) для препятствия:
) для препятствия:
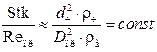 . (4.27)
. (4.27)
Таким образом, степень осаждения частиц за счет эффекта зацепления является зависимостью вида
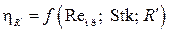 . (4.28)
. (4.28)
4.10. Поправка Кенингема-Милликена.
Броуновское движение частиц
Закон Стокса применим для движущихся частиц размерами более 1 мкм. Для более мелких частиц в уравнение (4.6) вводится поправка Кенингема-Милликена, учитывающая повышение подвижности частиц, размер которых сравним со средней длиной свободного пробега газовых молекул li:
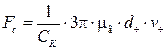 , (4.29)
, (4.29)
где поправка СК рассчитывается по уравнению
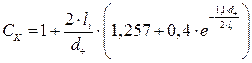 . (4.30)
. (4.30)
В свою очередь длину свободного пробега газовых молекул li можно оценить по следующему выражению:
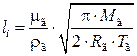 , (4.31)
, (4.31)
где 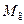 – масса 1 кмоль газов, кг/кмоль;
– масса 1 кмоль газов, кг/кмоль;
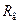 – универсальная газовая постоянная;
– универсальная газовая постоянная; 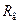 =8314 Дж/(кмоль×К);
=8314 Дж/(кмоль×К);
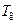 – абсолютная температура газов, К. Для воздуха, при нормальных условиях: tг = 20˚С (tг = 293˚К), ρг = 1,205∙кг/м3, μг = 1,82∙10–5 Па∙с и нормальном атмосферном давлении, длина пробега молекул li ≈ 6,5∙10–8 м.
– абсолютная температура газов, К. Для воздуха, при нормальных условиях: tг = 20˚С (tг = 293˚К), ρг = 1,205∙кг/м3, μг = 1,82∙10–5 Па∙с и нормальном атмосферном давлении, длина пробега молекул li ≈ 6,5∙10–8 м.
Ниже приведены значения поправок Ск, в соответствии с уравнением (4.30), для воздуха при нормальных условиях:
| dч, мкм | 0,003 | 0,01 | 0,03 | 0,1 | 0,3 | 1,0 | 3,0 | 10,0 |
| СК | 90,0 | 24,5 | 7,9 | 2,9 | 1,57 | 1,16 | 1,03 | 1,0 |
Кроме того, частицы субмикронных размеров (т.е. менее 1 мкм) подвержены воздействию броуновского (теплового) движения молекул газа. В этом случае направление перемещения частиц является случайным и описывается уравнением Эйнштейна, согласно которому амплитуду перемещения частицы Δx можно оценить по следующей формуле:
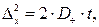 (4.32)
(4.32)
где Dч – коэффициент диффузии частицы, характеризующий интенсивность броуновского движения, м2/с;
t – время движения частицы, с.
При справедливости закона Стокса, когда размер частицы больше длины среднего пробега молекул (dч > li), коэффициент диффузии выражают как функцию размера частиц:
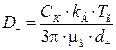 , (4.33)
, (4.33)
где kБ = 1,38∙10–23 Дж/К – постоянная Больцмана.
При dч > li коэффициент диффузии может быть рассчитан по формуле Лангмюра:
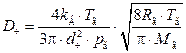 ,
,
где pг – абсолютное давление газов, Па.
В таблице 4.1 приведены скорости падения (седиментация) частиц и их смещение при броуновском движении за 1 с для нормальных условий.
Таблица 4.1
| Диаметр частиц, мкм | Критерий Рейнольдса | Скорость падения частицы, см/с | Броуновское перемещение частицы за 1 с |
| 0,6 0,2 0,06 0,02 | 1,32 13,2 0,366 1,43∙10-2 4,62∙10-2 2,45∙10-5 1,37∙10-6 1,26∙10-7 | 10,8 1,2 0,11 1,3∙10-2 1,39∙10-3 2,23∙10-4 4,16∙10-5 1,14∙10-5 | 5,04∙10-5 8,94∙10-5 1,54∙10-4 2,82∙10-4 5,07∙10-4 1,0∙10-3 2,1∙10-3 5,5∙10-3 1,06∙10-2 |
Как видно из таблицы, броуновское перемещение соизмеримо с перемещением при падении для частиц размером 1,0…0,6 мкм. Для частиц размером 0,06…0,02 мкм броуновское перемещение во много раз (в тысячи раз) превышает перемещение при свободном падении, и последнее практически уже не определяет характер движения частицы. Таким образом, высокодисперсная пыль и другие мелкие аэрозольные частицы практически не осаждаются даже в спокойном воздухе, а перемещаются во всем воздушном пространстве. Необходимо отметить, что все приведенные выше формулы относятся к частицам, имеющим правильную шаровидную форму. Поэтому и вводят понятие седиментацион-ного диаметра(разд. 2.1), который равен диаметру шарообразной частицы, имеющей одинаковую плотность и скорость осаждения с рассматриваемой частицей.
Следует также отметить, что рассмотренные зависимости определяют движение одиночной пылевой частицы в неограниченном пространстве. В действительности же, в одном объеме происходит осаждение большого числа частиц. Они взаимодействуют друг с другом, и это оказывает влияние на протекание процесса осаждения.
Объем воздушной среды ограничивается стенками или другими конструкциями (газоходы, воздуховоды, корпуса пылеочистного устройства и т.д.). Наличие такого рода ограничений воздушного пространства также вносит некоторые отклонения в приведенные зависимости.
Эффективность очистки газов при диффузионном осаждении оценивают при помощи безразмерных критериев, в которые входит коэффициент диффузии частиц Dч, – это критерий Шмидта Sc, характеризующий отношение сил внутреннего трения к диффузионным силам:
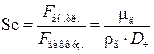 ,
,
и критерий Пекле Pe, характеризующий отношение конвективных сил к диффузионным силам:
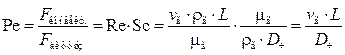 ,
,
где L – размер, характеризующий препятствие или обтекаемое тело.
Величина, обратная критерию Pe, называется параметром диффузионного осаждения и обозначается через D.
Для оценки эффективности диффузионного осаждения используют следующие формулы (при потенциальном, т.е. «гладком» обтекании препятствия):
при обтекании шара 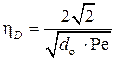 ;
;
при обтекании цилиндра 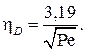
Согласно приведенным выражениям, эффективность диффузионного осаждения обратно пропорциональна размерам частицы и скорости газового потока:
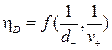 , или
, или 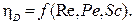 (4.34)
(4.34)
Дата добавления: 2021-06-28; просмотров: 941;











