Фракционная степень очистки газоочистительного аппарата

Значения коэффициентов степени очистки, которые могут быть получены в конкретных газоочистительных аппаратах, зависят от фракционного (дисперсного) состава улавливаемых частиц.

Фракционный коэффициент степени очистки равен отношению количества частиц рассматриваемой фракции, уловленной в аппарате, к количеству входящей в аппарат пыли той же фракции:

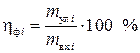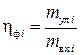, или , (3.6)

откуда массу уловленных частиц i-й фракции можно определить как

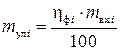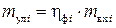, или (3.7)

Зная массу уловленных частиц i-й фракции, с учетом выражения (3.1) можно определить степень очистки аппарата в целом:

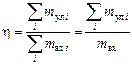, (3.8)

используя фракционный коэффициент очистки η_фi (формула (3.7)), выраже-
ние (3.8) можно переписать в следующем виде:

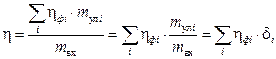, (3.9)

где коэффициент 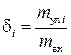– характеризует массовую долю уловленных частиц i-й фракции в аппарате к общей массе частиц на входе в аппарат.

Выражение (3.9) определяет общую степень (коэффициент) очистки в аппарате, если известны доли δ_i и фракционный коэффициент очистки η_фi по каждой фракции.

Рассмотрим выражение вида 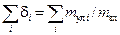, которое аналогично выражению (2.2): .

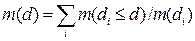Таким образом, если для рассматриваемых аэрозольных частиц и порошкообразных материалов справедлив закон логарифмически нормального распределения (2.3), то степень очистки аппарата можно определить с помощью интеграла вероятности:

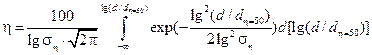, (3.10)

где lg(d/d_η=50) – отношение текущего размера частицы d к диаметру частиц d_η=50, осаждаемых с эффективностью η = 50 %;

lg σ_η – стандартное отклонение в функции распределения фракционного состава частиц пыли.

На практике степень очистки газоочистительного аппарата для рассматриваемых аэрозольных частиц с параметрами d₅₀ и σ_ч, как правило, определяют по известным параметрам тарировочной пыли d^т_η=50 и σ^т_η=50, при которых степень очистки аппарата для тарировочной пыли равна η^т = 50 %, в этом случае степень (коэффициент) очистки аппарата для пыли с параметрами d₅₀ и σ_ч принимается равной

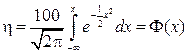, (3.11)

где параметр x имеет вид

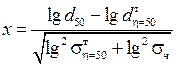; (3.12)

Ф(x) – функция нормального распределения Гаусса (Прил. 1).