Математические модели ламинарного и турбулентного пограничных слоев
Ламинарный пограничный слой имеет место при 1<<Rex<Rexкр. Математическая модель ламинарного стационарного двумерного пограничного слоя однородной сжимаемой жидкости включает следующие уравнения [2]:
- уравнение неразрывности
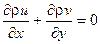 (3.1)
(3.1)
- уравнение движения в проекции на ось х (ось х направлена вдоль поверхности)
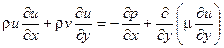 (3.2)
(3.2)
- уравнение движения в проекции на ось у (ось у совпадает с нормалью к поверхности)
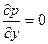 (3.3)
(3.3)
- уравнение энергии
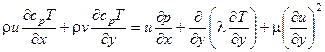 (3.4)
(3.4)
- уравнение состояния
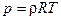 (3.5)
(3.5)
Система уравнений (3.1)-( 3.5) решается при следующих граничных условиях:
u = 0, v = 0, Т = Тw y = 0
u = uн, Т = Тн у = ∞ (3.6)
Уравнения (3.1)–(3.4) записаны в декартовой системе координат, причем ось х направлена вдоль поверхности, а ось у – по нормали к этой поверхности. В этих уравнениях: u и v – проекции вектора скорости на оси х и у, r – плотность, Т – температура, р – давление, m – динамический коэффициент вязкости, l – коэффициент теплопроводности, R – газовая постоянная газа, обтекающего тело. Индексом н обозначены параметры невозмущенного потока, а индексом w – параметры жидкости на поверхности.
Зависимость р=р(х) или значение градиента давления ∂р/∂х находится из уравнения движения внешнего по отношению к пограничному слою течения
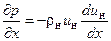 (3.7)
(3.7)
Уравнения (3.1)–(3.4) называются уравнениями Прандтля. Л.Прандтль получил их в результате упрощения дифференциальных уравнений Навье-Стокса, пренебрегая в этих уравнениях членами малого порядка по сравнению с оставшимися членами.
Математическая модель турбулентного пограничного слоя также как и математическая модель ламинарного пограничного слоя включает уравнения неразрывности, движения, энергии, к которым добавляются уравнение состояния и выражения для дополнительных членов уравнений, связанных с пульсациями параметров течения. Математическая модель стационарного двумерного турбулентного пограничного слоя однородной сжимаемой жидкости записывается следующим образом [2]:
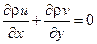 (3.8)
(3.8)
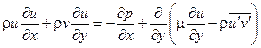 (3.9)
(3.9)
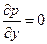 (3.10)
(3.10)
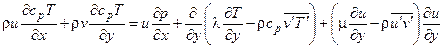 (3.11)
(3.11)
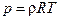 (3.12)
(3.12)
Граничные условия решения системы уравнений (3.8)–(3.12) записываются также как и граничные условия (3.6) уравнений Прандтля. Градиент давления ∂р/∂х находится из решения уравнения (3.7). Уравнения (3.8)–(3.12) описывают осредненное по времени турбулентное течение – все члены этих уравнений осреднены по времени.
Уравнения (3.8)–(3.11) называются уравнениями Рейнольдса. В отличие от уравнений Прандтля в правых частях этих уравнений присутствуют члены 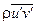 и
и 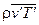 , обусловленные турбулентными пульсациями параметров жидкости в потоке. Под пульсацией какого-либо параметра жидкости понимается разность между мгновенным и осредненным по времени значением этого параметра. Величины
, обусловленные турбулентными пульсациями параметров жидкости в потоке. Под пульсацией какого-либо параметра жидкости понимается разность между мгновенным и осредненным по времени значением этого параметра. Величины 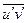 и
и 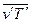 , представляющие собой осредненные по времени произведения соответствующих пульсационных параметров жидкости, называются моментами корреляции. Член
, представляющие собой осредненные по времени произведения соответствующих пульсационных параметров жидкости, называются моментами корреляции. Член 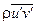 можно рассматривать как дополнительное (кажущееся) турбулентное касательное напряжение, а член
можно рассматривать как дополнительное (кажущееся) турбулентное касательное напряжение, а член 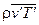 - как дополнительный тепловой поток, обусловленный пульсациями скорости и температуры жидкости [7, 10]:
- как дополнительный тепловой поток, обусловленный пульсациями скорости и температуры жидкости [7, 10]:
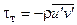 ,
, 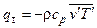 .
.
Для определения моментов корреляции 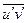 и
и 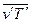 к настоящему времени разработано много так называемых моделей турбулентности, отличающихся различной сложностью. Одной из наиболее простых моделей турбулентности является модель пути перемешивания (смешения) Прандтля, описанная в Приложении 1. В соответствии с этой моделью
к настоящему времени разработано много так называемых моделей турбулентности, отличающихся различной сложностью. Одной из наиболее простых моделей турбулентности является модель пути перемешивания (смешения) Прандтля, описанная в Приложении 1. В соответствии с этой моделью
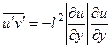 ,
, 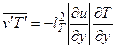 .
.
Здесь l – путь перемешивания для турбулентного переноса количества движения, lТ - путь перемешивания для турбулентного переноса тепла. Для пограничного слоя несжимаемой жидкости на поверхности можно принять lТ = l = ky (k – эмпирическая константа, равная 0,4 [2]).
Приведенные математические модели ламинарного и турбулентного пограничных слоев позволяют рассчитать все параметры жидкости в любой точке пограничного слоя.
При решении многих прикладных задач достаточно знать напряжение трения на поверхности τw, толщину пограничного слоя d и еще две условные толщины – толщину вытеснения d* и толщину потери импульса d**, которые определяются соответственно следующими выражениями:
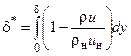 (3.13)
(3.13) 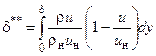 (3.14)
(3.14)
Толщина вытеснения – величина, численно равная расстоянию, на которое отодвигается от тела линия тока внешнего течения в результате вытесняющего действия пограничного слоя.
Толщина потери импульса – величина, численно равная толщине слоя, в каждом сечении которого жидкость с параметрами невозмущенного потока проносит секундное количество движения равное количеству движения, потерянному жидкостью в пограничном слое за счет уменьшения скорости (из-за трения).
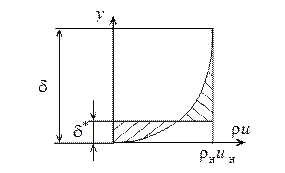 При известном поле (профиле) плотности тока (для несжимаемой жидкости - поле скорости) в поперечном сечении пограничного слоя толщину вытеснения можно найти, проведя линию, параллельную оси абсцисс так, чтобы заштрихованные площади на рис. 3.3 были равны.
При известном поле (профиле) плотности тока (для несжимаемой жидкости - поле скорости) в поперечном сечении пограничного слоя толщину вытеснения можно найти, проведя линию, параллельную оси абсцисс так, чтобы заштрихованные площади на рис. 3.3 были равны.
 Для определения напряжения на поверхности τw и толщин d, d* и d** можно использовать интегральный метод расчета пограничного слоя.
Для определения напряжения на поверхности τw и толщин d, d* и d** можно использовать интегральный метод расчета пограничного слоя.
Дата добавления: 2017-03-12; просмотров: 3349;











