Пограничный слой на поверхности

Изложение теории

При обтекании твердого тела реальной вязкой жидкостью всю область течения можно разбить на две качественно различные зоны:

а) зону, непосредственно прилегающую к обтекаемому телу, в которой имеют место явления диффузии, внутреннего трения и теплопроводности, обусловленные вязкостью, теплопроводностью жидкости и наличием градиентов концентрации, скорости и температуры [4, 7]:

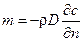- поток массы вещества, 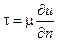- напряжение трения,

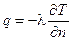- поток тепла

В этих формулах: D – коэффициент диффузии, м²/с; с – концентрация примеси (жидкости, составляющей смесь с основной жидкостью), с = r_пр/r (r_пр– плотность примеси, r – плотность смеси); l – коэффициент теплопроводности, Дж/(мּКּс); n – нормаль к поверхности тела.

Эта зона называется пограничным слоем.

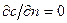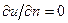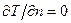б) набегающий невозмущенный поток и область, лежащую над пограничным слоем, в которых , и . Поэтому жидкость, текущую над пограничным слоем, можно считать идеальной (t = 0), в которой отсутствуют диффузия (m = 0) и теплопроводность (q = 0).

Таким образом, вместо одной сложной задачи решаются две более простые.

Часто поверхность, на которой образуется пограничный слой, является криволинейной. Но так как толщина пограничного слоя обычно намного меньше радиуса кривизны обтекаемой поверхности, то расчет пограничного слоя на криволинейной поверхности можно свести к расчету пограничного слоя на плоской поверхности, учтя изменение скорости и давления в невозмущенном потоке, обтекающем криволинейную поверхность. По этой причине ограничимся рассмотрением только пограничного слоя на плоской поверхности. Кроме этого будем считать, что поверхность тела является адиабатической (q_w = 0) и жидкость несжимаема (r = const).