Интегральный метод расчета пограничного слоя

Интегральный метод является универсальным – он применим как для расчета ламинарного, так и для расчета турбулентного пограничных слоев.

Этот метод основан на использовании уравнения Кармана, которое получается путем интегрирования по у дифференциальных уравнений пограничного слоя в частных производных, приведенных выше.

Уравнение Кармана в общем случае записывается следующим образом [2, 8]:

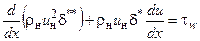
Для пограничного слоя на плоской поверхности (u_н = const , du_н/dx = 0, ρ_н = const) уравнение Кармана имеет вид

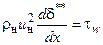(3.15)

Уравнение (3.15) содержит два неизвестных - d^** и t_w. Поэтому для его решения необходимо еще одно уравнение, которым является закон трения Ньютона

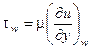(3.16)

Для определения (∂u/∂y)_w в уравнении (3.16) необходимо иметь выражение, описывающее изменение скорости в поперечных сечениях пограничного слоя, т.е. уравнение поля скоростей. Использование интегрального метода расчета возможно только для течений, поперечные поля которых обладают свойствами подобия и автомодельности. В случае пограничного слоя под подобием поперечных полей понимается совпадение безразмерных полей одноименных параметров в сходственных сечениях нескольких пограничных слоев, а под автомодельностью – независимость формы безразмерного поля некоторого параметра течения от продольной координаты х. В случае однофазных течений понятия подобия и автомодельности тождественны. Особенностью подобных и автомодельных течений является то, что для описания поперечного поля каждого параметра этих течений необходимо иметь только одно выражение, которое справедливо для любого сечения потока.

Подобие и автомодельность поперечных полей параметров жидкости имеют место в ламинарном и турбулентном пограничных слоях. В пределах переходного участка подобие и автомодельность отсутствуют.

Поле скоростей в ламинарном пограничном слое несжимаемой жидкости на плоской адиабатической поверхности хорошо аппроксимируется выражением [2, 8]

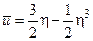(3.17)

в котором , .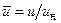

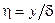В турбулентном пограничном слое вблизи обтекаемой поверхности число Рейнольдса, определенное по местным параметрам жидкости, может быть сколь угодно малым. Поэтому вблизи поверхности существует ламинарное течение. Эта часть пограничного слоя называется ламинарным подслоем. В нем скорость меняется по линейному закону

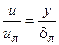
Здесь: u_л – скорость на границе ламинарного подслоя, d_л – его толщина.

Ламинарный подслой очень тонкий d_л/d ~ 0,01, но скорость на его границе относительно велика: u_л/u_н ~ 0,5.

Формулу для расчета поля скоростей в основной части турбулентного пограничного слоя можно получить, интегрируя выражение

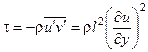, l = ky

В результате интегрирования получаем

.

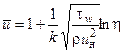Этой формулой пользоваться неудобно, так как необходимо знать t_w. Обычно для описания поля скоростей в турбулентном пограничном слое используется формула [2, 8]

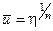, (3.18)

в которой n зависит от Re. При Re = 10⁶…10⁸ можно принять n = 7.

Используя уравнение Кармана (3.15), уравнение Ньютона (3.16), выражения (3.13) и (3.14) для d^* и d^**, формулы (3.17) и (3.18), описывающие изменение скорости в поперечных сечениях ламинарного и турбулентного пограничных слоев, можно получить формулы для расчета t_w, d, d^* и d^**. В случае течения несжимаемой жидкости вдоль плоской адиабатической поверхности эти формулы имеют вид:

для ламинарного пограничного слоя

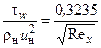
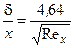
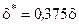
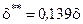
для турбулентного пограничного слоя

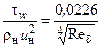
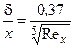
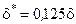
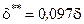
В приведенных формулах: 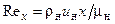, 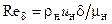. Значения коэффициентов в правых частях формул для турбулентного пограничного слоя соответствуют диапазону изменения числа Рейнольдса Re_x = 10⁶…10⁸, при котором показатель степени в формуле (3.18) равен 1/7.