Режимы течения жидкостей
Изложение теории
В зависимости от механизма переноса массы, количества движения и энергии в потоке жидкости различают два режима ее течения: ламинарный и турбулентный. При определенных условиях возможен переход ламинарного режима течения в турбулентный. Этот переход происходит не сразу, а на некотором участке течения, который называют переходным. Течение в пределах этого участка сочетает в себе особенности и ламинарного и турбулентного режимов течения. Часто принимают, что переход ламинарного течения в турбулентное происходит в некотором переходном сечении.
Возможность существования ламинарного или турбулентного режима течения определяется значением безразмерного комплекса, называемого критерием или числом Рейнольдса
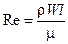
в котором: W, r и m - скорость, плотность и коэффициент динамической вязкости жидкости, l - характерный размер течения.
Значение числа Рейнольдса, при котором происходит переход ламинарного течения в турбулентное, называется критическим. При течении жидкости в трубе за характерный размер принимается диаметр трубы, а критическое число Рейнольдса равно 2300 (Reкр=2300). Т.е. принимается, что если Re<Reкр, то течение ламинарное, а если Re>Reкр, то течение турбулентное.
Ламинарное течение - упорядоченное слоистое течение, в котором обмен массой, количеством движения и энергией между соседними слоями жидкости осуществляется за счет молекулярного переноса - перемещения отдельных молекул жидкости из слоя в слой. При ламинарном двумерном течении жидкости вдоль оси х, при котором параметры жидкости в поперечном сечении потока меняются только вдоль оси у, а вдоль оси z остаются неизменными в плоскости площадки, параллельной плоскости x0z (рис. 2.1), действует касательное напряжение (напряжение трения) [2, 7, 8]
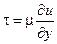 , (2.1)
, (2.1)
а через единицу площади этой площадки в единицу времени переносится масса m и количество тепла q [4, 7]
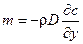 (2.2)
(2.2) 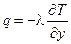 (2.3).
(2.3).
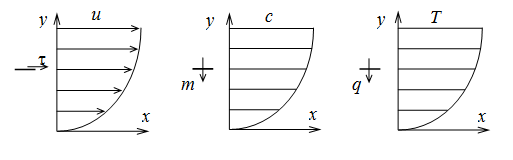
Рис. 2.1. Касательное напряжение, потоки массы и тепла, обусловленные градиентами
параметров течения
В формулах (2.1)-(2.3): m, D и l - коэффициенты динамической вязкости, диффузии и теплопроводности; u, T и с - проекция вектора скорости на ось х, температура жидкости и массовая концентрация примеси (жидкости, подмешанной к основной жидкости). Массовая концентрация примеси равна отношению плотности примеси rпр к плотности смеси жидкостей r: с = rпр/r. Знаки "+" и "-" в правых частях формул (2.1)-(2.3) проставлены с учетом знаков производных и направлением векторов 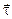 ,
, 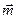 и
и 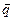 . В частности, удельные потоки массы
. В частности, удельные потоки массы 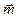 и тепла
и тепла 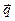 направлены в сторону, противоположную положительному направлению градиентов концентрации с и температуры Т.
направлены в сторону, противоположную положительному направлению градиентов концентрации с и температуры Т.
Следует отметить, что в случае ламинарного течения коэффициенты m и l являются физическими свойствами конкретных жидкостей, а коэффициент D - свойством их конкретных смесей. Значения этих коэффициентов могут быть определены по таблицам теплофизических свойств жидкостей и смесей жидкостей.
Турбулентное течение - хаотическое неупорядоченное и, следовательно, не стационарное течение, в котором обмен массой, количеством движения и энергией между рядом расположенными слоями жидкости происходит не только за счет молекулярного переноса, но главным образом за счет перемещения из слоя в слой целых объемов жидкости, которые называют молями.
Турбулентное течение можно представить как течение, в котором на главное слоистое движение жидкости накладывается хаотическое перемещение вдоль и поперек главного направления движения жидкости постоянно образующихся и исчезающих вихрей различного размера. При этом под "вихрями" следует понимать жидкие объемы вихревого происхождения. В турбулентном потоке сначала образуются вихри, размер которых соизмерим с размерами потока, например радиусом трубы, струи и т.п. В процессе своего движения эти вихри распадаются на более мелкие, при распаде которых образуются еще более мелкие вихри и т.д. В крупных вихрях инерционные явления преобладают над вязкими. Такие вихри определяют процессы переноса массы, количества движения и тепла, но в малой степени подвержены действию вязкости. Непрерывное уменьшение размера вихрей в конечном итоге приводит к появлению мелких вихрей, внутри которых вязкие силы преобладают над силами инерции. В мелких вихрях вязкие силы совершают работу трения, которая преобразуется в тепло, идущее на нагрев жидкости. Как говорят, происходит диссипация энергии, переход кинетической энергии в тепло. При этом полная механическая энергия жидкости, которая может быть затрачена на совершение полезной работы, уменьшается.
При математическом описании турбулентных течений часто используется их разложение на осредненное (слоистое) движение и пульсационное (хаотическое) движение, вызванное перемещением вихрей. При этом действительное течение с характерными для него извилистыми хаотически переплетающимися линиями тока и траекториями, заменяется некоторым упорядоченным "слоистым" течением. Линии тока пульсационного движения пересекают линии тока осредненного движения, проникают из одного слоя осредненного течения в другой и создают при этом перемешивание жидкости сквозь площадки, расположенные вдоль линий тока осредненного течения. Это перемешивание сопровождается переносом сквозь границу между слоями жидкости массы, количества движения и энергии осредненного течения. Перенос количества движения создает турбулентное трение между слоями, перенос тепла определяет турбулентную теплопроводность, перенос примеси - диффузию этой примеси.
При разложении турбулентного движения на осредненное и пульсационное движения вводятся средние и пульсационные величины каждого параметра состояния жидкости [2, 10]:
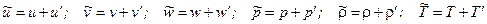 (2.4)
(2.4)
Здесь: u, v, w - проекции вектора скорости жидкости 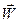 на оси координат x, y и z; p, r и Т - давление, плотность и температура. Волнистой чертой сверху обозначены мгновенные величины, а штрихом - пульсационные.
на оси координат x, y и z; p, r и Т - давление, плотность и температура. Волнистой чертой сверху обозначены мгновенные величины, а штрихом - пульсационные.
Под осредненным значением f какого-либо параметра жидкости 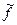 понимается величина [2, 10]
понимается величина [2, 10]
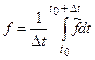 (2.5)
(2.5)
Для осреднения по времени t промежуток времени Dt должен быть достаточно большим, чтобы осредненное значение не зависело от времени. При этом 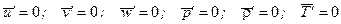 . Черта сверху означает осреднение по времени.
. Черта сверху означает осреднение по времени.
При выводе уравнений, описывающих турбулентное течение, исходными уравнениями являются уравнения, записанные для мгновенных значений параметров жидкости. В этих уравнениях делается замена мгновенных значений всех величин на их осредненные и пульсационные значения с использованием выражений (2.4), после чего выполняется осреднение по времени членов полученных уравнений с применением правил осреднения Рейнольдса [2, 10]:
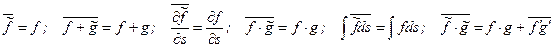
Осредненное по времени произведение пульсационных величин 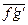 называется моментом корреляции. Момент корреляции определяет связь между изменением случайных величин
называется моментом корреляции. Момент корреляции определяет связь между изменением случайных величин 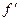 и
и 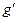 . Если случайные величины независимы, то
. Если случайные величины независимы, то 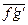 =0; для зависимых величин
=0; для зависимых величин 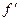 и
и 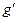
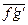 ¹0.
¹0.
После проведения временного осреднения в уравнениях, описывающих турбулентные течения, вследствие нелинейности исходных уравнений появляются члены вида 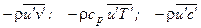 , которые можно рассматривать как дополнительные турбулентные напряжения, тепловые потоки и потоки массы, обусловленные пульсациями параметров жидкости.
, которые можно рассматривать как дополнительные турбулентные напряжения, тепловые потоки и потоки массы, обусловленные пульсациями параметров жидкости.
Покажем это на примере величины 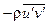 . Рассмотрим в турбулентном потоке несжимаемой жидкости, имеющей нулевую осредненную скорость, площадку dF с нормалью, параллельной оси х (оси у и z лежат в плоскости этой площадки). Массовый расход жидкости через эту площадку равен
. Рассмотрим в турбулентном потоке несжимаемой жидкости, имеющей нулевую осредненную скорость, площадку dF с нормалью, параллельной оси х (оси у и z лежат в плоскости этой площадки). Массовый расход жидкости через эту площадку равен 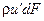 . Пересекая площадку, жидкость переносит через нее определенное количество движения. Мгновенное значение этого количества движения в единицу времени в проекции на ось у равно
. Пересекая площадку, жидкость переносит через нее определенное количество движения. Мгновенное значение этого количества движения в единицу времени в проекции на ось у равно 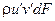 , а осредненное по времени -
, а осредненное по времени - 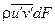 . В результате переноса количества движения через выбранную площадку (изменения количества движения при переходе через нее) появляется поверхностная сила, действующая на площадку. При рассмотрении изменения количества движения в проекции на ось у эта сила равна произведению напряжения, действующего в плоскости площадки dF вдоль оси у, на площадь dF. Это напряжение является касательным напряжением. Обозначим его осредненное по времени значение
. В результате переноса количества движения через выбранную площадку (изменения количества движения при переходе через нее) появляется поверхностная сила, действующая на площадку. При рассмотрении изменения количества движения в проекции на ось у эта сила равна произведению напряжения, действующего в плоскости площадки dF вдоль оси у, на площадь dF. Это напряжение является касательным напряжением. Обозначим его осредненное по времени значение 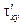 (штрих указывает на то, что это напряжение вызвано пульсациями жидкости; первый индекс указывает направление нормали к площадке, в которой действует напряжение, а второй индекс - ось, вдоль которой напряжение направлено). Тогда в соответствии с уравнением количества движения можно записать
(штрих указывает на то, что это напряжение вызвано пульсациями жидкости; первый индекс указывает направление нормали к площадке, в которой действует напряжение, а второй индекс - ось, вдоль которой напряжение направлено). Тогда в соответствии с уравнением количества движения можно записать 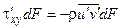 или
или
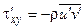 .
.
В общем случае в турбулентном потоке действуют девять напряжений, обусловленных пульсациями скорости: три нормальных и шесть касательных, три из которых попарно равны [7, 10]:
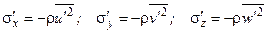
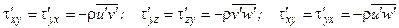 (2.6)
(2.6)
Эти напряжения называются кажущимися напряжениями турбулентного течения или напряжениями Рейнольдса, так как уравнения турбулентного течения, в которых присутствуют эти напряжения, впервые выведены О.Рейнольдсом.
Пульсационное движение со скоростями u', v' и w' влияет на осредненное движение u, v и w таким образом, что в осредненном движении как бы увеличивается сопротивление возникновению деформаций. Другими словами, действие пульсационного движения на осредненное движение проявляется как бы в увеличении вязкости осредненного движения. Эту вязкость называют кажущейся вязкостью.
В турбулентном течении дополнительный поток массы, вызванный пульсациями параметров жидкости, имеет проекции [7, 10]
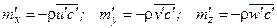 (2.7)
(2.7)
а дополнительный поток тепла – проекции [7, 10]
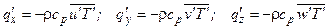 (2.8)
(2.8)
Основная проблема при расчете турбулентных течений заключается в том, чтобы выразить моменты корреляции, входящие в правые части выражений (2.6)-(2.8), через параметры течения. Существует большое количество так называемых моделей турбулентности различной сложности, позволяющих это сделать. Одна из самых первых и наиболее простых моделей турбулентности называется моделью пути перемешивания (или смешения) Прандтля. Эта модель турбулентности рассматривается в Приложении 1. В соответствии с моделью турбулентности Прандтля в случае двумерного течения момент корреляции 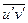 равен
равен
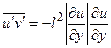 (2.9)
(2.9)
и кажущееся турбулентное напряжение определяется выражением
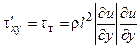 (2.10)
(2.10)
Величина l называется путем перемешивания (или смешения) Прандтля. Выражение для кажущегося турбулентного напряжения (2.10) можно записать по аналогии с напряжением молекулярного трения (2.1), введя кажущуюся вязкость mт
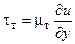 ;
; 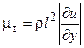 (2.11)
(2.11)
Эта вязкость не зависит от природы жидкости, а определяется видом (типом) течения, так как от вида течения зависит выражение для пути перемешивания l. При течении жидкости вдоль твердой поверхности (пограничный слой на поверхности твердого тела) [2]
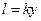
k - постоянная, равная 0,4.
В турбулентной круглой свободной струе [3]
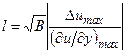
Dumax и (¶u/¶y)max - максимальные разность скоростей и градиент скорости в рассматриваемом сечении струи, В - константа, равная 0,013.
Аналогично (2.11) для дополнительных турбулентных потоков тепла и массы можно записать
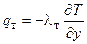 ;
; 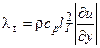 (2.12)
(2.12) 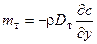 ;
; 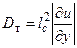 (2.13)
(2.13)
lТ и lc - пути перемешивания по температуре и концентрации; из опыта известно, что lТ =lc.
Объединяя (2.11) с (2.1), (2.12) с (2.2) и (2.13) с (2.3), можно написать выражения для суммарного напряжения трения, суммарных потоков тепла и массы в двумерном турбулентном течении
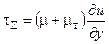 ;
; 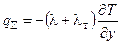 ;
; 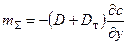
2.2. Лабораторная работа "Экспериментальное исследование режимов течения жидкости в трубе"
Цель работы - определение критического числа Рейнольдса, при котором происходит переход ламинарного режима течения в турбулентный при движении жидкости в трубе.
Дата добавления: 2017-03-12; просмотров: 3421;











