Сверхзвуковое течение с непрерывным увеличением скорости (течение Прандтля-Майера)

Изложение теории

Течение Прандтля-Майера реализуется при обтекании сверхзвуковым потоком внешнего тупого угла (180°+d). На рис. 3.1 приведена фотография обтекания клина, полученная теневым методом.

Ось клина составляет некоторый угол i с направлением вектора скорости невозмущенного потока. В этом случае на верхней поверхности клина образуется косой скачок уплотнения, а на нижней – центрированная волна разрежения, пересекая которую сверхзвуковой поток ускоряется.

Рассмотрим обтекание сверхзвуковым потоком поверхности, образованной двумя полубесконечными пластинами, расположенными под углом d_ст друг к другу, т.е. образующими внешний тупой угол АВС, равный (180°+d_ст) (рис. 3.2).

Будем считать, что вдоль адиабатической стенки АС течет сверхзвуковой (l_н > 1) равномерный параллельный поток идеального газа. В этом случае течение вдоль стенки АС будет энергетически изолированным (Т^* = const) и изоинтропическим (р^* = const).

Вершина угла С является источником слабых возмущений, которые в виде бесчисленного множества прямолинейных характеристик разрежения располагаются в пределах угла НСК. Совокупность этих характеристик называется центрированной волной разрежения, так как все образующие ее характеристики исходят из одной точки. Первая характеристика СН располагается под углом 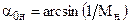к вектору скорости невозмущенного потока 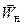, а последняя СК – под углом 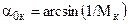к вектору скорости после поворота потока .

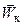На каждой характеристике разрежения нормальная составляющая скорости W_n увеличивается, а тангенциальная составляющая W_t остается неизменной. Это можно показать, записав уравнение количества движения в проекциях на нормаль к фронту характеристики и на направление характеристики [4]. Бесконечно малое увеличение модуля вектора скорости газа на характеристике разрежения (за счет увеличения W_n) сопровождается бесконечно малым уменьшением давления, плотности, температуры и скорости звука при постоянных полной температуре и полном давлении. Течение газа в пределах угла НСК является результатом пересечения газом бесконечного числа характеристик разрежения. Поэтому вдоль линии тока газа, пересекающего пучок характеристик (волну разрежения), его полная температура и полное давление остаются постоянными (Т^* = const, р^* = const), а скорость и статические параметры плавно изменяются как это показано на рис. 3.2. Так как параметры потока вдоль каждой характеристики не меняются, то поток газа при его течении в пределах угла НСК будет равномерным и параллельным.

Можно дать и другое объяснение характера изменения параметров газа в течении Прандтля-Майера без выделения в волне разрежения отдельных характеристик. Изменение скорости газа в течении Прандтля-Майера следует рассматривать как результат геометрического воздействия на сверхзвуковой поток. Площадь поперечного сечения потока, ограниченного стенкой АCВ и некоторой линией тока на рис. 3.2, увеличивается в направлении течения. В соответствии с уравнением обращения воздействий увеличение площади сверхзвукового потока приводит к его ускорению. Изменение параметров газа в течении Прандтля-Майера является следствием перераспределения энергии газа между отдельными ее видами. Так как рассматриваемое течение – энергетически изолированное течение (в нем отсутствует техническая работа и обмен теплом с окружающей средой), то в соответствии с уравнением энергии полная энергия газа остается неизменной. При увеличении скорости газа увеличивается его кинетическая энергия, что при постоянной полной энергии приводит к уменьшению потенциальной энергии давления и внутренней энергии газа. По этой причине давление и температура газа в течении Прандтля-Майера уменьшаются.

Предположим, что после поворота поток движется вдоль адиабатической стенки СВ, т.е. d_к = d_ст (d_к – угол поворота потока). Этот поток является равномерным и параллельным, в котором все параметры газа, в том числе полная температура и полное давление, остаются постоянными.

Таким образом, во всей области течения – вдоль стенки АВ, в пределах угла НСК и вдоль стенки СВ – течение равномерное и параллельное с постоянными параметрами торможения (Т^* = const, р^* = const, r^* = const).

Так как течение Прандтля-Майера представляет собой течение вокруг вершины угла (точки С) и вдоль характеристик, исходящих из этой вершины, параметры потока остаются неизменными, то все формулы для расчета течения Прандтля-Майера выводятся в полярных координатах (r, j), где r – радиус-вектор точки, j – угол, образованный этим радиусом-вектором с некоторым лучом, соответствующим началу отсчета угла j.

В связи с тем, что параметры торможения газа в течении Прандтля-Майера не меняются, то статические параметры газа и его скорость в любой точке линии тока могут быть рассчитаны по формулам

Т = Т^* t(l) , р = р^* p(l),r = r^* e(l) , W = a_кр l.

Чтобы воспользоваться этими формулами, надо знать значение приведенной скорости l в каждой точке линии тока, пересекающей волну разрежения, т.е необходимо иметь зависимость l = l(j). Формула, связывающая значение приведенной скорости l с полярным углом j имеет вид [1, 4]:

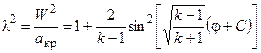(3.1)

в которой С – постоянная интегрирования.

Для расчета приведенной скорости l необходимо определить значение константы С или, что то же самое, найти начало отсчета угла j.

3.1.1. Частный случай течения при l_н = 1

При М_н=1 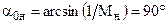, т.е. в этом случае первая характеристика перпендикулярна вектору скорости невозмущенного потока, и ее удобно принять за начало отсчета угла j, т.е. для нее j = 0. Подстановка l_н = 1 и j = 0 в формулу (3.1) дает С = 0 и эта формула принимает вид

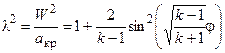(3.2)

Угол поворота потока d, полярный угол j и угол характеристики a₀ связаны уравнением [1, 4]

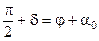, (3.3)

в котором .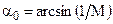

Линии тока в полярных координатах описываются уравнением [1, 4]:

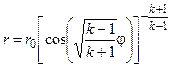, (3.4)

В уравнении (3.4) r₀ – радиус-вектор линии тока при j=0.

Совместное решение уравнений (3.2) и (3.3), записанных для последней характеристики, позволяет для заданного значения угла поворота потока d_к=d_ст определить приведенную скорость потока после поворота l_к или же по значению l_к найти угол поворота d_к. При этом давление потока после его поворота должно быть вполне определенным и равным р_к = р^*×p(l_к). На практике часто заданными являются давления р_к и р^*, отношение которых определяет значение приведенной скорости l_к. Эта приведенная скорость связана с р_к и р^* соотношением

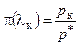(3.5)

В этом случае необходимо совместно решать уравнения (3.2), (3.3) и (3.5), в результате чего находятся значения l_к, d_ки j_к. Если окажется, что d_к < d_ст, то поток будет двигаться не вдоль поверхности СВ, а вдоль луча, располагающегося под углом d_к к своему первоначальному направлению. Это явление называется отрывом сверхзвукового потока.

В течении Прандтля-Майера газ ускоряется, но его скорость не может превышать максимальной скорости

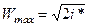или .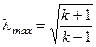

Дальнейшее ускорение и поворот потока оказываются невозможными. Отсюда следует, что должны существовать максимальные углы j_max и d_max. Значение j_max можно получить из формулы (3.2), если в нее подставить l_max :

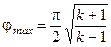(3.6)

Значение d_max получается в результате подстановки в формулу (3.3) j_max:

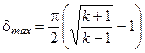(3.7)

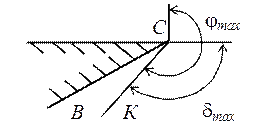
Если d_к > d_max и истечение происходит в вакуум (рис. 3.3), то поток поворачивает только на угол d_max и течет не по стенке СВ, а по лучу СК, соответствующему d_max. Между этой характеристикой СК и стенкой СВ образуется пространство ВСК, в котором отсутствуют молекулы газа исходного потока.

3.1.2. Расчет течения Прандтля-Майера при l_н > 1

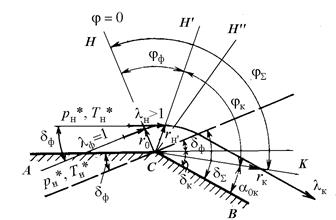Расчет течения Прандтля-Майера при l_н>1 (рис. 3.4) проводится с использованием формул, полученных для случая l_н = 1. Правомерность этого обусловлена тем, что вдоль каждой характеристики параметры потока остаются постоянными, т.е. на любой характеристике поток является равномерным и параллельным. И, следовательно, для поворота потока, происходящего правее данной характеристики (например СН¢¢) не имеет значение, начался поворот потока сразу при значении l_н > 1 (на характеристике СН) или же до этого поток разгонялся от l_ф = 1 до l_н > 1 при повороте на угол d_ф. Поэтому при расчете течения Прандтля-Майера при l_н > 1 принимают, что данный сверхзвуковой поток получен в результате предварительного ускорения фиктивного звукового потока l_ф=1, р_ф*=р_н*, Т_ф* = Т_н* при его повороте на угол d_ф и при повороте характеристики СН на угол j_ф. Течение между характеристиками СН и СК будет одинаково как для заданного потока l_н > 1, так и для фиктивного l_ф = 1.

Для фиктивного потока справедливо уравнение (3.3), которое в этом случае принимает вид:

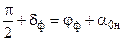(3.8)

Таким образом для расчета течения Прандтля-Майера при l_н>1 можно использовать формулы, полученные для случая l_н = 1, подставив в них вместо углов j и d суммарные углы j_S = j + j_ф и d_S = d + d_ф:

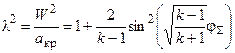(3.9)

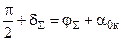(3.10)

В формуле (3.10) a_0к – угол между последней характеристикой и вектором скорости потока после его поворота; .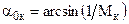

Вычитая из уравнения (3.10) уравнение (3.8), получаем уравнение, связывающее углы jи d:

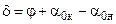
Формулы (3.6) и (3.7) для максимальных углов поворота потока, полученные для случая l_н = 1, справедливы при l_н > 1 лишь для суммарных углов

,

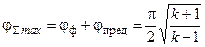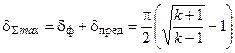
Максимальные углы поворота сверхзвукового потока и характеристики от их первоначального направления называются предельными; их величина уменьшается с увеличением l_н: d_пред = d_Smax – d_ф; j_пред = j_Smax – j_ф.

3.2. Лабораторная работа "Теоретическое и экспериментальное исследование течения Прандтля-Майера"

Цель работы - теоретическое и экспериментальное исследование изменения параметров газа в течении Прандтля-Майера. После обработки экспериментальных данных и проведения теоретических расчетов должны быть получены зависимости М_к=f₁(d_к) и р_к/р_н=f₂(d_к), которые представляются в виде графиков, позволяющих сравнить результаты расчета и эксперимента.