Газовые течения при наличии внешних воздействий.
Закон обращения воздействий
Изложение теории
Параметры газового потока изменяются только при воздействии на него окружающей среды. При этом возможны следующие воздействия окружающей среды на газ (газодинамическую систему):
1. геометрическое dF > 0 или dF < 0 (расширение или сужение канала);
2. расходное dG > 0 или dG < 0 (подвод или отвод массы газа);
3. тепловое dqн > 0 или dqн < 0 (подвод или отвод тепла);
4. механическое dlтех > 0 или dlтех < 0 (работа турбины или компрессора);
5. воздействие трения dlтр > 0, которое проявляется в форме подвода к газу тепла dqтр, выделяющегося в результате трения и равного работе трения dlтр.
В зависимости от знака каждого воздействия это воздействие противоположным образом влияет на параметры дозвукового и сверхзвукового течений. О том, как влияет то или иное воздействие на параметры дозвукового или сверхзвукового потока можно определить по уравнению закона обращения воздействий. Это уравнение получается из совместного решения системы четырех уравнений – неразрывности, энергии в тепловой форме, энергии в механической форме (уравнения Бернулли) и состояния, записанных в дифференциальном виде:
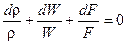 (4.1) dqн - dlтех = срdT+ WdW (4.2)
(4.1) dqн - dlтех = срdT+ WdW (4.2)
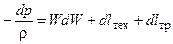 (4.3)
(4.3) 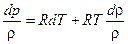 (4.4)
(4.4)
В уравнениях (4.1)–(4.4): W, p, T и r - скорость, давление, температура и плотность газа, R – удельная газовая постоянная, F – площадь поперечного сечения канала, lтр- гидравлические потери (работа сил трения, связанная с вязкостью газа), cp – удельная теплоемкость при постоянном давлении.
Следует отметить, что уравнения (4.1)–(4.3) записаны для элементарной струйки (одномерного течения) при условии постоянного расхода газа (dG = 0).
Подставляя в уравнение (4.4) dr/r, dT и dp/r, выраженные из уравнений (4.1), (4.2) и (4.3), соответственно, и учитывая, что ср = kR/(k – 1), а2 = kRT, M = W/a, получаем:
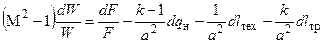 (4.5)
(4.5)
В этом уравнении: М – число Маха, а – скорость звука, k – показатель адиабаты.
Уравнение (4.5) называется уравнением закона обращения воздействий. В нем отсутствует член, описывающий расходное воздействие, так как исходные уравнения (4.1) – (4.3) записаны для случая dG = 0.
В левой части уравнения (4.5) стоит дифференциал скорости dW, знак которого определяет поведение скорости: при dW>0 поток ускоряется (конфузорное течение), а при dW<0 – тормозится (диффузорное течение). В правой части уравнения находятся члены, описывающие воздействия на систему со стороны окружающей среды. Все воздействия, за исключением воздействия трения, могут менять знак на противоположный; воздействие трения всегда имеет положительный знак, являясь односторонним воздействием. Знак скобки (М2 - 1) в левой части уравнения при переходе через скорость звука меняется на противоположный. Это означает, что для того, чтобы сохранить знак dW при переходе через скорость звука необходимо знак воздействия сменить на противоположный.
В соответствии с уравнением (4.5):
1. любое физическое воздействие одинакового знака противоположным образом влияет на дозвуковые и сверхзвуковые газовые течения;
2. переход через скорость звука с помощью одностороннего воздействия не возможен. Это явление называется кризисом течения;
3. переход через скорость звука возможен только в том случае, если в критическом сечении знак воздействия изменить на противоположный.
Уравнения типа (4.5) могут быть получены для любого из параметров состояния газа – р, Т и r.
При течении газа в камерах сгорания реактивных двигателей на газ одновременно оказывается тепловое воздействие и воздействие трения. Поэтому рассмотрим каждое из этих воздействий в отдельности и их совместное влияние на газовый поток. При этом будем считать, что газ движется в канале постоянного сечения и течение является одномерным и стационарным, т.е. его параметры меняются только вдоль оси канала и не зависят от времени.
При воздействии на газодинамическую систему одного трения уравнение (4.5) принимает вид:
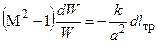 (4.6)
(4.6)
| М < 1 | - | + | - | + | |
| М > 1 | + | - | - | + |
Уравнение закона обращения воздействий используется, как правило, либо для определения характера изменения какого-либо параметра состояния системы при заданных воздействиях на систему, либо для определения знаков внешних воздействий, обеспечивающих заданное изменение параметров системы. Определим с помощью уравнения (4.6) как меняется скорость дозвукового потока газа в трубе с трением. При М<1 скобка в левой части этого уравнения имеет знак «минус». Так как dlтр>0 и перед правой частью уравнения (4.6) стоит знак «минус», то правая часть этого уравнения отрицательна. Левая и правая части любого уравнения должны иметь одинаковые знаки. Поэтому для того, чтобы левая часть уравнения была отрицательной дифференциал скорости должен быть положительным – dW>0, т.е. наличие трения приводит к ускорению дозвукового потока. Сверхзвуковой поток, наоборот, за счет трения тормозится.
Из уравнения (4.6) можно получить уравнение, связывающее приведенные скорости газа в двух сечениях трубы с постоянной площадью поперечного сечения при наличии трения. Для этого необходимо выразить dlтр через скорость потока по формуле Дарси-Вейсбаха [4]
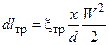 (4.7)
(4.7)
и перейти от W и Mк l:
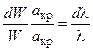 ;
; 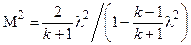
В формуле (4.7): W – скорость газа, х – расстояние от начала трубы до рассматриваемого сечения, xтр – коэффициент трения, являющийся функцией числа Рейнольдса Re = rWd/m (W, r и m - скорость, плотность и динамический коэффициент вязкости газа, d - диаметр трубы).
В результате получается обыкновенное дифференциальное уравнение первого порядка относительно приведенной скорости l, интегрирование которого при условии xтр =const приводит к уравнению:
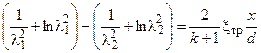 (4.8)
(4.8)
В этом уравнении: l1 – значение приведенной скорости в начале трубы при х = 0, l2– значение приведенной скорости в произвольном сечении трубы на расстоянии х = х2 от ее начала. С помощью уравнения (4.8) можно определить значение приведенной скорости в произвольном сечении трубы, если известны приведенная скорость в начале трубы l1, диаметр трубы d, коэффициент трения xтр и показатель адиабаты k.
Введем функцию 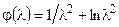 и назовем безразмерную величину, находящуюся в правой части уравнения (4.8)
и назовем безразмерную величину, находящуюся в правой части уравнения (4.8)
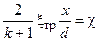
приведенной длиной трубы. Тогда уравнение (4.8) можно представить в виде
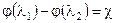 (4.9)
(4.9)
При дозвуковом течении газа в трубе с трением скорость газа по длине трубы возрастает и максимальное значение скорости соответствует выходному сечению трубы. При значении c = cкр, называемом критическим, на выходе из трубы достигается скорость звука (М2 = l2 = 1) и уравнение (4.9) принимает вид:
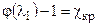 (4.10)
(4.10)
Если c < cкр, то на всей длине трубы, включая ее выходное сечение, l < 1. Если c > cкр, то уравнение (4.9) не имеет решения для l2. Это означает, что принятое начальное значение l1 не может быть реализовано. Данное явление называется кризисом воздействия трения. При приведенной длине трубы c, превышающей cкр, не зависимо от значения c на срезе трубы сохраняется кризис - l2 = 1. Увеличение приведенной длины трубы в этом случае приводит к увеличению потерь полного давления по длине трубы и, следовательно, к уменьшению полного давления на выходе из трубы р2*. В соответствии с выражением для массового расхода 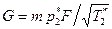 (m - коэффициент, зависящий от k и R; F - площадь поперечного сечения трубы; Т* - полная температура), записанным для случая l2 = 1, при уменьшении р2* уменьшается расход газа. Таким образом, увеличение c в области c > cкр приводит к уменьшению расхода газа через трубу и, как следствие этого, - к уменьшению приведенной скорости на входе в трубу до значения l1¢ (при изменении длины трубы остальные параметры газа на входе в трубу остаются неизменными). Приведенная скорость l1¢ при заданной величине c находится по формуле, полученной из уравнения (4.10), в которое вместо l1 подставляется l¢1, а вместо cкр - c (в этом случае c представляет собой cкр для приведенной скорости l¢1):
(m - коэффициент, зависящий от k и R; F - площадь поперечного сечения трубы; Т* - полная температура), записанным для случая l2 = 1, при уменьшении р2* уменьшается расход газа. Таким образом, увеличение c в области c > cкр приводит к уменьшению расхода газа через трубу и, как следствие этого, - к уменьшению приведенной скорости на входе в трубу до значения l1¢ (при изменении длины трубы остальные параметры газа на входе в трубу остаются неизменными). Приведенная скорость l1¢ при заданной величине c находится по формуле, полученной из уравнения (4.10), в которое вместо l1 подставляется l¢1, а вместо cкр - c (в этом случае c представляет собой cкр для приведенной скорости l¢1):
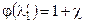 , (4.11)
, (4.11)
 Значение приведенной скорости, определенной по уравнению (4.11), является максимальным значением приведенной скорости l1max на входе в трубу с приведенной длиной c. Реально могут существовать только течения с l1 £ l1max. На рис. 4.1 кривой 1 представлена зависимость l1max от безразмерной длины трубы x/d для дозвукового потока воздуха при Т1* = 300К, р1* = 0,1 МПа и d = 0,02 м.
Значение приведенной скорости, определенной по уравнению (4.11), является максимальным значением приведенной скорости l1max на входе в трубу с приведенной длиной c. Реально могут существовать только течения с l1 £ l1max. На рис. 4.1 кривой 1 представлена зависимость l1max от безразмерной длины трубы x/d для дозвукового потока воздуха при Т1* = 300К, р1* = 0,1 МПа и d = 0,02 м.
 Следует отметить, что определенным значениям приведенных скоростей l1 и l2 в уравнении (4.8) должны соответствовать определенные значения давлений р1 и р2. При изменении длины трубы для того, чтобы получить значение l2, соответствующее уравнению (4.8) при сохранении постоянными значений р1 и l1, необходимо изменять давление в выходном сечении трубы.
Следует отметить, что определенным значениям приведенных скоростей l1 и l2 в уравнении (4.8) должны соответствовать определенные значения давлений р1 и р2. При изменении длины трубы для того, чтобы получить значение l2, соответствующее уравнению (4.8) при сохранении постоянными значений р1 и l1, необходимо изменять давление в выходном сечении трубы.
При одном тепловом воздействии на систему уравнение (4.6) записывается следующим образом:
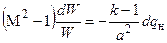 (4.12)
(4.12)
| М < 1 | - | + | - | + | |
| М > 1 | + | - | - | + |
В соответствии с этим уравнением подвод тепла к дозвуковому потоку приводит к увеличению, а к сверхзвуковому потоку – к уменьшению скорости газа.
Будем считать, что тепло подводится к идеальному газу, движущемуся с дозвуковой скоростью. Подвод тепла к движущемуся газу (даже идеальному) приводит к уменьшению его полного давления. Это явление называется тепловым сопротивлением. Тепловое сопротивление объясняется тем, что при подводе тепла к движущемуся газу энтропия возрастает в большей степени, чем при подводе того же количества тепла к неподвижному газу вследствие различия в Т и Т*:
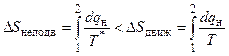 (Т < Т*)
(Т < Т*)
Изменение полного давления в необратимом процессе однозначно связано с изменением энтропии – увеличение энтропии приводит к уменьшению полного давления.
 Отношение полных температур газа на выходе из трубы Т2* и на входе в трубу Т1* называется подогревом: q = Т2*/Т1*. При некотором значении подогрева qкр = Т2кр*/Т1*, который называется критическим, на выходе из трубы (в ее сечении 2) скорость газа становится звуковой (М2 = l2 = 1). Если продолжать подогревать газ в этой трубе дальше, то приведенная скорость в этом сечении меняться не будет (l2=1), а расход, определяемый выражением
Отношение полных температур газа на выходе из трубы Т2* и на входе в трубу Т1* называется подогревом: q = Т2*/Т1*. При некотором значении подогрева qкр = Т2кр*/Т1*, который называется критическим, на выходе из трубы (в ее сечении 2) скорость газа становится звуковой (М2 = l2 = 1). Если продолжать подогревать газ в этой трубе дальше, то приведенная скорость в этом сечении меняться не будет (l2=1), а расход, определяемый выражением 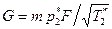 , уменьшится вследствие уменьшения р2* и возрастания Т2* из-за увеличения подогрева. Это явление называется тепловым кризисом. Для того чтобы предотвратить тепловой кризис необходимо либо устранить тепловое воздействие, либо изменить его знак на противоположный. Уменьшение расхода газа при подогреве, превышающем критический, приведет к уменьшению скорости газа в начальном сечении трубы. И чем больше этот подогрев, тем меньше скорость на входе в трубу. Зависимость qкр = q(l1) для l1 < 1 приведена на рис. 4.2. Кривая q = qкр соответствует кризису течения, при котором l2=1. Под кривой расположена область подогревов q < qкр, соответствующих l2<1, а над кривой – область неосуществимых при данных l1 подогревов. При этих подогревах q > qкр на срезе трубы сохраняется кризис l2 = 1, а расход газа G и приведенная скорость l1 автоматически снижаются до значений G¢ и l1¢, для которых данный подогрев будет критическим.
, уменьшится вследствие уменьшения р2* и возрастания Т2* из-за увеличения подогрева. Это явление называется тепловым кризисом. Для того чтобы предотвратить тепловой кризис необходимо либо устранить тепловое воздействие, либо изменить его знак на противоположный. Уменьшение расхода газа при подогреве, превышающем критический, приведет к уменьшению скорости газа в начальном сечении трубы. И чем больше этот подогрев, тем меньше скорость на входе в трубу. Зависимость qкр = q(l1) для l1 < 1 приведена на рис. 4.2. Кривая q = qкр соответствует кризису течения, при котором l2=1. Под кривой расположена область подогревов q < qкр, соответствующих l2<1, а над кривой – область неосуществимых при данных l1 подогревов. При этих подогревах q > qкр на срезе трубы сохраняется кризис l2 = 1, а расход газа G и приведенная скорость l1 автоматически снижаются до значений G¢ и l1¢, для которых данный подогрев будет критическим.
 При одновременном тепловом воздействии и воздействии трения на систему уравнение закона обращения воздействий имеет вид:
При одновременном тепловом воздействии и воздействии трения на систему уравнение закона обращения воздействий имеет вид:
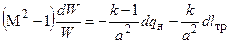 (4.13)
(4.13)
При дозвуковом течении как наличие трения, так и подвод тепла к газу приводят к увеличению его скорости. При заданных значениях подогрева q и приведенной длины трубы c существует максимальное значение приведенной скорости на входе в трубу l1max, соответствующее кризису течения, при котором l2=1. Чем больше c и q, тем меньше значение l1max. Зависимость l1max от подогрева q и безразмерной длины трубы x/d для дозвукового потока воздуха при Т1* = 300К, р1* = 0,1 МПа и d = 0,02 м приведена на рис. 4.1. Точки пересечения кривых q=const с осью ординат (x/d=0) соответствуют максимальной приведенной скорости на входе в трубу при одном тепловом воздействии. При фиксированном значении подогрева q увеличение безразмерной длины трубы x/d приводит к уменьшению l1max. Для заданной безразмерной длины трубы (x/d=const) l1max тем меньше, чем больше подогрев q.

 При совместном действии на газ трения и подогрева соотношение подведенного к газу тепла и работы трения зависит от безразмерной длины трубы, величины подогрева и скорости газа на входе в трубу. На рис. 4.3 приведена зависимость отношения подведенного тепла к работе трения от безразмерной длины трубы и приведенной скорости на входе в трубу при критическом режиме течения (l2=1) и подогреве q=2. Как видно из рисунка, отношение qн/lтр может меняться в широких пределах. При большой длине трубы (x/d ~ 150…200), на срезе которой имеет место кризис течения, работа трения составляет порядка 10% от количества подведенного тепла. Пренебрежение трением при расчете параметров течения в трубе в этом случае может привести к существенным ошибкам в расчетах.
При совместном действии на газ трения и подогрева соотношение подведенного к газу тепла и работы трения зависит от безразмерной длины трубы, величины подогрева и скорости газа на входе в трубу. На рис. 4.3 приведена зависимость отношения подведенного тепла к работе трения от безразмерной длины трубы и приведенной скорости на входе в трубу при критическом режиме течения (l2=1) и подогреве q=2. Как видно из рисунка, отношение qн/lтр может меняться в широких пределах. При большой длине трубы (x/d ~ 150…200), на срезе которой имеет место кризис течения, работа трения составляет порядка 10% от количества подведенного тепла. Пренебрежение трением при расчете параметров течения в трубе в этом случае может привести к существенным ошибкам в расчетах.
При течении вязкого "холодного" газа в трубе, на концах которой зафиксированы давления, скорость газа по длине трубы будет возрастать от скорости на входе до скорости на выходе из трубы. Если подогревать газ в этой трубе, то его расход через трубу уменьшится вследствие уменьшения плотности газа на выходе из трубы – расход будет определяться параметрами газа в выходном сечении трубы, в котором задано давление. Уменьшение расхода приведет к уменьшению скорости на входе. При сравнении изменения скорости по длине трубы с заданными давлениями на ее концах при наличии только трения и при наличии трения и подогрева оказывается, что в случае комбинированного воздействия (трения и подогрева) скорость на входе в трубу меньше, но производная dW/dx в трубе больше по сравнению со случаем одного воздействия трения.
Расчет всех параметров течения газа в трубе при воздействии на газ только трения или только подогрева в одномерной постановке может быть выполнен по формулам, приведенным в [1, 4]. В случае совместного теплового воздействия и воздействия трения на одномерный поток газа необходимо решать систему обыкновенных дифференциальных уравнений, записанных с учетом трения газа о стенку канала и теплообмена между газом и стенкой. При этом находятся средние по сечению канала параметры. Следует отметить, что результаты расчетов газовых течений в трубах, выполненные по одномерным моделям, хорошо согласуются с экспериментальными данными.
При наличии трения и подогрева изменение приведенной скорости и коэффициента потерь полного давления по длине трубы можно легко рассчитать при известных законах изменения статического давления p и полной температуры Т* вдоль трубы (изменение р и Т* по длине трубы может быть найдено экспериментально; для этого необходимо измерить их в нескольких сечениях трубы). При энергетически изолированном течении газа в трубе с трением нужно знать изменение только статического давления по длине трубы.
Формулы для расчета li и si в произвольном i-ом сечении трубы получаются из уравнения неразрывности, записанного через статические и полные давления для начального и текущего (i-го) сечений трубы. В общем случае уравнение неразрывности записывается следующим образом [4]:
- через статические давления
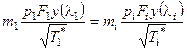 (4.14)
(4.14)
- через полные давления
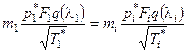 (4.15)
(4.15)
В уравнениях (4.14) и (4.15): m – коэффициент, зависящий от k и R [для воздуха m = 0,0404 (кг×К/Дж)1/2], у(l) и q(l) – газодинамические функции.
При течении газа неизменного состава в трубе с постоянной площадью поперечного сечения mi=m1 и Fi=F1. В этом случае из уравнения (4.14) получаем
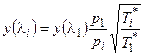 (4.16)
(4.16)
а из уравнения (4.15) -
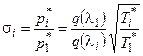 (4.17)
(4.17)
При отсутствии подогрева и наличии только трения выражения (4.16) и (4.17) упрощаются:
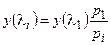 (4.18)
(4.18) 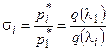 (4.19)
(4.19)
При совместном воздействии на газ трения и подогрева по измеренным в эксперименте статическому давлению и полной температуре в конкретном сечении трубы выражение (4.16) позволяет определить значение газодинамической функции у(li) для этого сечения трубы. Величина приведенной скорости li находится по у(li) с помощью таблиц газодинамических функций. Полученное значение li используется для расчета si по формуле (4.17). При наличии одного воздействия трения в эксперименте достаточно провести изменение только статического давления. В этом случае для расчета li и si используются формулы (4.18) и (4.19).
Для того чтобы воспользоваться формулами (4.16)–(4.19) необходимо знать приведенную скорость в начальном сечении трубы l1. Эта скорость может быть найдена по газодинамической функции p(l):
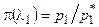 .
.
Если в трубу засасывается неподвижный газ с давлением В0 за счет создания разрежения на выходе из трубы, то вследствие того, что процесс ускорения газа от нулевой скорости до скорости во входном сечении трубы является энергетически изолированным и изоэнтропическим р1* = В0. В этом случае
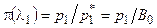 (4.20)
(4.20)
Значение l1 определяется по значению газодинамической функции p(l1) с использованием таблиц газодинамических функций.
4.2. Лабораторная работа "Экспериментальное исследование течения вязкого газа в трубе с трением и подогревом"
Цель работы - изучение влияния трения и подогрева на параметры газа, движущегося в цилиндрической трубе постоянного поперечного сечения. В результате выполнения работы должны быть получены зависимости приведенной скорости l и коэффициента потерь полного давления s от безразмерной длины трубы 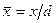 при воздействии на поток только трения и совместного воздействия трения и подогрева.
при воздействии на поток только трения и совместного воздействия трения и подогрева.
Дата добавления: 2017-03-12; просмотров: 4292;











