Уравнение движения поезда.

Перейдем к реальному поезду, состоящему из локомотива и вагонов общим числом N, соединенных между собой и с локомотивом посредством автосцепок, которые представляют собой упруго-жесткие связи. Реальный поезд в продольном направлении имеет число степеней свободы, равное числу вагонов в поезде из-за различия характеристик поглощающих аппаратов и различного износа деталей автосцепных приборов. Следовательно, вагоны могут перемещаться друг относительно друга и относительно центра тяжести поезда.

Рассмотрим поступательное движение поезда под воздействием внешних сил:

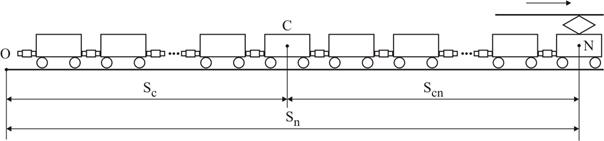
s_c – координата центра тяжести поезда относительно начала координат;

s_n – координата центра тяжести n-го вагона относительно начала координат;

s_cn – координата центра тяжести n-го вагона относительно центра тяжести поезда.

s_c характеризует поступательное перемещение поезда, s_cn – относительное перемещение вагонов, на которое дополнительно расходуется энергия.

Координату центра тяжести любого вагона можно определить как сумму координаты центра тяжести поезда относительно начала отсчета и координаты центра тяжести этого вагона относительно центра тяжести поезда. Поезд в целом характеризуется системой уравнений:

.

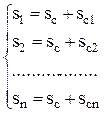Ускорение n-го вагона складывается из ускорения центра тяжести поезда и ускорения n-го вагона относительно центра тяжести поезда. Для нахождения ускорения n-го вагона дважды продифференцируем выражение по времени:

.

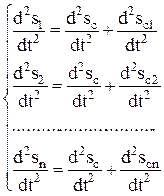Подставляя полученные выражения для ускорения в уравнение движения, выведенное в п.1.1, получим:

.

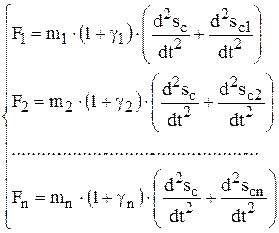Таким образом, движение поезда характеризуется системой из n дифференциальных уравнений. В практических расчетах практически никогда не используют приведенное выше выражение, т.к. получить выражение для относительных перемещений вагонов крайне сложно. Для этого необходимо использовать аппарат теории вероятностей и математической статистики.